2022-2023学年湖北省荆门市高一（下）期末数学试卷

一、单选题：本大题共8小题，每小题5分，共40分．在每小题给出的四项中，只有一项是符合题目要求的．

• 1．下列函数是偶函数的为（　　）

  A．y=2x

  B． y = lo g 1 2 x

  C．y=x-1

  D．y=x2
  组卷：112引用：1难度：0.7

  解析

• 2．已知复数z满足z²+2z+2=0，则|z|=（　　）

  A．1

  B．2

  C． 2

  D． 5
  组卷：30引用：2难度：0.7

  解析

• 3．总体由编号为01，02，03，…，19，20的20个个体组成，利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第3列开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（　　）
  

  78 16 65 72 08    02 63 14 07 02    43 69 97 28 01    98

  32 04 92 34 49    35 82 00 36 23    48 69 69 38 74    81

  A．08

  B．07

  C．02

  D．01
  组卷：263引用：3难度：0.8

  解析

• 4．圆锥被一平面所截得到一个圆台，若圆台的上底面半径为2cm,下底面半径为3cm,圆台母线长为4cm,则该圆锥的侧面积为（　　）

  A．28πcm2

  B．36πcm2

  C．42πcm2

  D．48πcm2
  组卷：109引用：4难度：0.7

  解析

• 5．垃圾分类的目的是提高垃圾的资源价值和经济价值，力争物尽其用，进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会、经济、生态等几方面的效益．已知某种垃圾的分解率v与时间t（月）满足函数关系式v=a•b^t（其中a,b为非零常数）．若经过6个月，这种垃圾的分解率为5%，经过12个月，这种垃圾的分解率为10%，那么这种垃圾完全分解（分解率为100%）至少需要经过（　　）（参考数据lg2≈0.3）

  A．20个月

  B．28个月

  C．32个月

  D．40个月
  组卷：48引用：1难度：0.5

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  x 2 - 2 x + 2 ，	x ≥ 0
  x + 2 ，	x ＜ 0

  ，若方程f（x）=a有三个不等的实数根x₁，x₂，x₃，则x₁+x₂+x₃的取值范围为（　　）

  A．（-2，0）

  B．（-1，1）

  C．（0，1）

  D．（1，2）
  组卷：201引用：1难度：0.5

  解析

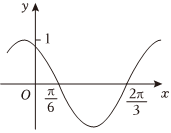• 7．如图是函数f（x）=sin（ωx+φ）的部分图象．现将f（x）的图象向右平移m（m＞0）个单位长度后得到奇函数g（x），则m的最小值为（　　）

  A． π 3

  B． 2 π 3

  C． π 6

  D． π 12
  组卷：97引用：2难度：0.7

  解析

四、解答题：本题共6题，共70分，解答应写出文字说明，证明过程或演算步骤．

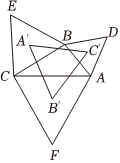• 21．拿破仑定理是法国著名军事家拿破仑•波拿巴最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆圆心恰为另一个等边三角形（此等边三角形称为拿破仑三角形）的顶点．”已知在△ABC中，以BC，AC，AB为边向外作三个等边三角形，其外接圆圆心依次记为A′，B′，C′．若角A，B，C的对边分别为a,b,c,且

  acos

  C

  +

  3

  asin

  C

  -

  b

  -

  c

  =

  0

  ．
  （1）求A；
  （2）若

  a

  =

  3

  ，求△A′B′C′的面积最大值．
  组卷：161引用：3难度：0.2

  解析

• 22．已知

  f

  （

  x

  ）

  =

  lo

  g

  1

  2

  x

  +

  x

  +

  1

  x

  -

  1

  ．
  （1）求

  f

  （

  2

  ）

  +

  f

  （

  1

  2

  ）

  +

  f

  （

  3

  ）

  +

  f

  （

  1

  3

  ）

  的值；
  （2）求证f（x）有且仅有两个零点x₁，x₂，并求x₁x₂的值；
  （3）若g（x）=x²-ax+9，对任意的x₁∈[2，+∞），x₂∈[1，4]，不等式f（x₁）≤g（x₂）恒成立，求a的取值范围．
  组卷：37引用：2难度：0.6

  解析