2022-2023学年河北省邯郸市高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={-1，0，1}，B={x|x²-3x+2=0}，则A∪B=（　　）

  A．{1}

  B．{1，2}

  C．{-1，0，1}

  D．{-1，0，1，2}
  组卷：106引用：1难度：0.7

  解析

• 2．已知复数z=2+i,且

  az

  -

  z

  +

  b

  =

  0

  ，其中a,b为实数，则（　　）

  A．a=-1，b=-4

  B．a=-1，b=4

  C．a=1，b=-4

  D．a=1，b=4
  组卷：77引用：5难度：0.8

  解析

• 3．已知向量

  a

  ，

  b

  满足

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  |

  a

  +

  2

  b

  |

  =

  13

  ，则

  a

  •

  b

  =（　　）

  A．1

  B．2

  C．-1

  D．-2
  组卷：52引用：2难度：0.7

  解析

• 4．开普勒第一定律也称椭圆定律、轨道定律，其内容如下：每一行星沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点上．将某行星H看作一个质点，H绕太阳的运动轨迹近似成曲线

  x

  2

  m

  +

  y

  2

  n

  =1（m＞n＞0），行星H在运动过程中距离太阳最近的距离称为近日点距离，距离太阳最远的距离称为远日点距离．若行星H的近日点距离和远日点距离之和是18（距离单位：亿千米），近日点距离和远日点距离之积是16，则m+n=（　　）

  A．39

  B．52

  C．86

  D．97
  组卷：63引用：4难度：0.7

  解析

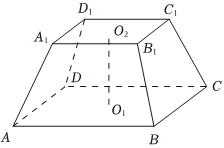• 5．如图，在四棱台ABCD-A₁B₁C₁D₁中，正方形ABCD和A₁B₁C₁D₁的中心分别为O₁和O₂，O₁O₂⊥平面ABCD，O₁O₂=3，AB=5，A₁B₁=4，则直线O₁O₂与直线AA₁所成角的正切值为（　　）

  A． 2 3

  B． 2 6

  C． 3 6

  D． 6 6
  组卷：125引用：4难度：0.8

  解析

• 6．已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=e^x-2+2x-5，则不等式xf（x）＞0的解集是（　　）

  A．（-2，0）∪（2，+∞）	B．（-∞，-2）∪（0，2）
  C．（-2，0）∪（0，2）	D．（-∞，-2）∪（2，+∞）
  组卷：116引用：3难度：0.6

  解析

• 7．在一个3×3宫格中，有如图所示的初始数阵，若从中随机选择2个宫格，将其相应的数字变成相反数，得到新的数阵，则新的数阵中所有数字之和为25的概率为（　　）
  

  1	2	3
  4	5	6
  7	8	9

  A． 1 9

  B． 3 18

  C． 2 9

  D． 1 3
  组卷：10引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）经过点P（4，2），双曲线C的右焦点F到其渐近线的距离为2．
  （1）求双曲线C的方程；
  （2）已知Q（0，-2），D为PQ的中点，作PQ的平行线l与双曲线C交于不同的两点A，B，直线AQ与双曲线C交于另一点M，直线BQ与双曲线C交于另一点N，证明：M，N，D三点共线．
  组卷：177引用：5难度：0.3

  解析

• 22．已知函数f（x）=3e^x-aln（x+1）．
  （1）若f（x）是增函数，求a的取值范围；
  （2）若f（x）-sinx≥3在[0，+∞）上恒成立，求a的取值范围．
  组卷：69引用：2难度：0.5

  解析