2022-2023学年吉林省长春十七中高二（下）期末数学试卷
发布：2024/6/30 8:0:9
一、单选题（本题8小题，每小题5分，满分40分）
-
1．sin2023°cos73°+cos43°sin73°=（ ）
组卷：222引用：3难度：0.7 -
2．已知函数f（x）=2lnx+8x,则
的值为（ ）limΔx→0f（1+2Δx）-f（1）Δx组卷：15引用：1难度：0.8 -
3．已知
，则sin（π3+α）=23的值等于（ ）cos（7π6-α）组卷：476引用：3难度：0.7 -
4．曲线f（x）=x+cosx在点
处的切线斜率为（ ）（π2，f（π2））组卷：152引用：2难度：0.8 -
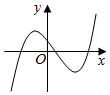5．函数y=f（x）的导函数y=f′（x）的图象如图所示，则函数y=f（x）的图象可能是（ ）组卷：5083引用：71难度：0.9 -
6．已知函数f（x）=aex-lnx在区间（1，2）上单调递增，则a的最小值为（ ）
组卷：5468引用：35难度：0.7 -
7．已知α为锐角，cosα=
，则sin1+54=（ ）α2组卷：5903引用：18难度：0.8
四.解答题（本题6小题，满分70分）
-
21．已知函数
为奇函数，且f（x）图象的相邻两对称轴间的距离为f（x）=3sin（ωx+φ）+2sin2（ωx+φ2）-1（ω＞0，0＜φ＜π）．π2
（1）求f（x）的解析式和单调递增区间．
（2）将函数f（x）的图象向右平移个单位长度，再把横坐标缩小为原来的π6（纵坐标变），得到函数y=g（x）的图象，当12时，求函数g（x）的值域．x∈[-π12，π6]
（3）设h（x）=f（x）+sinx+cosx,若h（x）≤c恒成立，求实数c的最小值．组卷：12引用：1难度：0.4 -
22．随着时代发展和社会进步，教师职业越来越受青睐，考取教师资格证成为不少人的就业规划之一．当前，中小学教师资格考试分笔试和面试两部分．已知某市2021年共有10000名考生参加了中小学教师资格考试的笔试，现从中随机抽取100人的笔试成绩作为样本，整理得到如表频数分布表：
（1）假定笔试成绩不低于90分为优秀，若从上述样本中笔试成绩不低于80分的考生里随机抽取2人，求至少有1人笔试成绩为优秀的概率；笔试成绩X [40，50） [50，60） [60，70） [70，80） [80，90） [90，100] 人数 5 15 35 30 10 5
（2）由频数分布表可认为该市全体考生的笔试成绩X近似服从正态分布N（μ，δ2），其中μ近似为100名样本考生笔试成绩的平均值（同一组中的数据用该组区间的中点值代替），δ2=180，据此估计该市全体考生中笔试成绩不低于82.4的人数（结果四舍五入精确到个位）；
（3）考生甲为提升综合素养报名参加了某拓展知识竞赛，该竞赛要回答3道题，前两题是哲学知识，每道题答对得3分，答错得0分；最后一题是心理学知识，答对得4分，答错得0分．已知考生甲答对前两题的概率都是，答对最后一题的概率为12，且每道题答对与否相互独立，求考生甲的总得分Y的分布列及数学期望．（参考数据：23；若X～N（μ，δ2），则P（μ-δ＜X＜μ+δ）≈0.6827，P（μ-2δ＜X＜μ+2δ）≈0.9545，P（μ-3δ＜X＜μ+3δ）≈0.9973）180≈13.4组卷：50引用：2难度：0.5
