2023-2024学年重庆市杨家坪中学高二（上）第一次月考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知点A（2，5），B（1，6），则直线AB的倾斜角为（　　）

  A． 3 π 4

  B． 2 π 3

  C． π 3

  D． π 4
  组卷：436引用：7难度：0.8

  解析

• 2．已知圆的方程是x²+y²-2x-1=0，则它的半径是（　　）

  A．1

  B． 2

  C．2

  D．4
  组卷：285引用：4难度：0.5

  解析

• 3．直线x+2ay-5=0与直线ax+4y+2=0平行，则a的值为（　　）

  A．2

  B．±2

  C． 2

  D． ± 2
  组卷：340引用：2难度：0.9

  解析

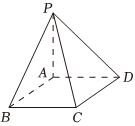• 4．《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为（　　）

  A． 125 2 π 3

  B．50π

  C．100π

  D． 500 π 3
  组卷：334引用：4难度：0.6

  解析

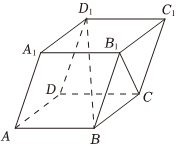• 5．如图，平行六面体ABCD-A₁B₁C₁D₁中，AB=2，AD=3，AA₁=3，∠BAD=∠BAA₁=∠DAA₁=

  π

  3

  ，则B₁C与BD₁所成角的大小为（　　）

  A． π 4

  B． π 3

  C． π 2

  D． 2 π 3
  组卷：129引用：6难度：0.7

  解析

• 6．已知直线l₁：x-my+1=0过定点A，直线l₂：mx+y-m+3=0过定点B，l₁与l₂相交于点P，则|PA|²+|PB|²=（　　）

  A．10

  B．13

  C．16

  D．20
  组卷：748引用：10难度：0.7

  解析

• 7．若平面内两定点A，B间的距离为2，动点P满足

  |

  PA

  |

  |

  PB

  |

  =

  3

  ，则|PA|²+|PB|²的最大值为（　　）

  A． 3 + 3

  B． 7 + 4 3

  C． 8 + 4 3

  D． 16 + 8 3
  组卷：86引用：5难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤。

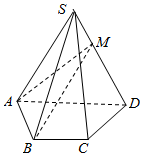• 21．如图，在四棱锥S-ABCD中，侧面SAD为等边三角形，底面ABCD为等腰梯形，且AB=BC=CD=1，AD=2，SA=SB．
  （1）证明：平面SAD⊥平面ABCD；
  （2）若点M在棱SD上，且二面角M-AB-D的大小为

  π

  4

  ，求

  DM

  MS

  的值．
  组卷：84引用：2难度：0.6

  解析

• 22．正方形ABCD中，AB=4，点O为正方形内一个动点，且

  OA

  =

  2

  ，设

  ∠

  OAB

  =

  θ

  ，

  （

  θ

  ∈

  （

  0

  ，

  π

  2

  ）

  ）

  ．
  （1）当

  θ

  =

  π

  3

  时，求OB²+OD²的值；
  （2）若P为平面ABCD外一点，满足

  ∠

  POA

  =∠

  POB

  =∠

  POD

  =

  π

  2

  ，

  PO

  =

  2

  ，记cos∠BPD=f（θ），求f（θ）的取值范围．
  组卷：84引用：3难度：0.5

  解析