2022-2023学年黑龙江省哈尔滨九中高一(下)月考数学试卷(3月份)
发布:2024/6/12 8:0:8
一、单选题,本大题共有8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.
=( )sin5π4组卷:20引用:3难度:0.9 -
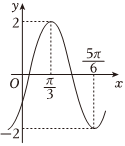 2.函数的一部分图象如图所示,此函数的解析式为( )y=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)组卷:116引用:2难度:0.7
2.函数的一部分图象如图所示,此函数的解析式为( )y=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)组卷:116引用:2难度:0.7 -
3.下列是函数f(x)=tan(2x-
)的对称中心的是( )π4组卷:643引用:7难度:0.7 -
4.已知
,则向量|m|=6,|n|=3,m•n=-12在向量m方向上的投影向量的长度为( )n组卷:53引用:3难度:0.8 -
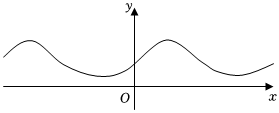 5.已知函数y=f(x)的图像如图所示,则f(x)的解析式可能是( )组卷:99引用:4难度:0.7
5.已知函数y=f(x)的图像如图所示,则f(x)的解析式可能是( )组卷:99引用:4难度:0.7 -
6.已知△ABC是边长为1的正三角形,
=2BD,DC+AB=2AC,则AE=( )AE•AD组卷:217引用:8难度:0.7 -
7.记某时钟的中心点为O,分针针尖对应的端点为A.已知分针长OA=5cm,且分针从12点位置开始绕中心点O顺时针匀速转动.若以中心点O为原点,3点和12点方向分别为x轴和y轴正方向建立平面直角坐标系,则点A到x轴的距离y(单位:cm)与时间t(单位:min)的函数解析式为( )
组卷:126引用:3难度:0.7
三、解答题(本大题共有6小题,共70分.解答应写出文字说明、证明过程和演算步骤)
-
21.已知函数
,且当x∈[0,π]时,f(x)的最大值为f(x)=acos2(π-x)-2sin(π+x)-9a8(a∈R).14
(1)求a的值;
(2)设函数,若对任意的x1∈[0,π],总存在g(x)=bcos(x+π6),使得f(x1)=g(x2),求实数b的取值范围.x2∈[-π3,π2]组卷:82引用:4难度:0.5 -
22.定义非零向量
=(a,b)的“相伴函数”为f(x)=asinx+bcosx(x∈R),向量OM=(a,b)称为函数f(x)=asinx+bcosx(x∈R)的“相伴向量”(其中O为坐标原点).记平面内所有向量的“相伴函数”构成的集合为S.OM
(1)设h(x)=cos(x+3)+3cos(π6-x)(x∈R),请问函数h(x)是否存在相伴向量π3,若存在,求出与OM共线的单位向量;若不存在,请说明理由.OM
(2)已知点M(a,b)满足:],向量ba∈(0,3的“相伴函数”f(x)在x=x0处取得最大值,求tan2x0的取值范围.OM组卷:404引用:8难度:0.1


