2023-2024学年天津市滨海新区塘沽紫云中学高二（上）第一次月考数学试卷

一、单选题（本大题共13小题，每题5分，共65分。）

• 1．一条直线过点A（1，0）和B（-2，3），则该直线的倾斜角为（　　）

  A．30°

  B．45°

  C．135°

  D．150°
  组卷：589引用：7难度：0.7

  解析

• 2．已知

  a

  =（-3，2，5），

  b

  =（1，x,-1），且

  a

  •

  b

  =2，则x的值是（　　）

  A．6

  B．5

  C．4

  D．3
  组卷：1622引用：27难度：0.9

  解析

• 3．直线x-3y+1=0的一个方向向量是（　　）

  A．（1，-3）

  B．（1，3）

  C．（3，-1）

  D．（3，1）
  组卷：330引用：4难度：0.8

  解析

• 4．若直线l₁：x+ay+6=0与l₂：（a-2）x+3y+2a=0平行，则l₁与l₂间的距离为（　　）

  A． 2

  B． 8 2 3

  C． 3

  D． 8 3 3
  组卷：3042引用：47难度：0.7

  解析

• 5．如图，在平行六面体ABCD-A₁B₁C₁D₁中，若

  B

  D

  1

  =x

  AB

  +y

  AD

  +z

  A

  A

  1

  ，则（x,y,z）=（　　）

  A．（-1，1，1）

  B．（1，-1，1）

  C．（1，1，-1）

  D．（-1，-1，-1）
  组卷：589引用：13难度：0.8

  解析

• 6．已知圆x²+y²+2x-2y+a=0截直线x+y+2=0所得弦的长度为4，则实数a的值是（　　）

  A．-2

  B．-4

  C．-6

  D．-8
  组卷：10245引用：79难度：0.9

  解析

• 7．已知点A（-1，1）、B（1，2）、C（0，-1），过点C的直线l与线段AB有公共点，则直线l斜率k的取值范围是（　　）

  A．[-2，3]	B．[-2，0）∪（0，3]
  C．（-∞，-2]∪[3，+∞）	D．以上都不对
  组卷：643引用：7难度：0.7

  解析

三、解答题（本大题共4小题，共55分。解答应写出文字说明，证明过程或演算步骤）

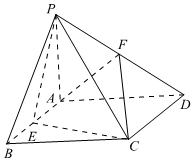• 22．如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是矩形，E、F分别是AB、PD的中点．若PA=AD=3，CD=

  6

  ．
  （Ⅰ）求证：AF∥平面PCE；
  （Ⅱ）求点F到平面PCE的距离；
  （Ⅲ）求直线FC平面PCE所成角的正弦值．
  组卷：456引用：10难度：0.5

  解析

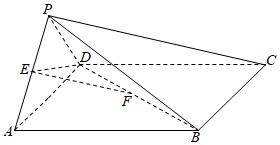• 23．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，E，F分别为PA，BD中点，PA=PD=AD=2．
  （Ⅰ）求证：EF∥平面PBC；
  （Ⅱ）求二面角E-DF-A的余弦值；
  （Ⅲ）在棱PC上是否存在一点G，使GF⊥平面EDF？若存在，指出点G的位置；若不存在，说明理由．
  组卷：464引用：11难度：0.5

  解析