2023年贵州省铜仁市思南中学高考数学模拟试卷
发布:2024/7/14 8:0:9
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知定义在[0,+∞)上的函数f(x)满足
,且当x∈[0,2)时,f(x)=-x2+2x.设f(x)在[2n-2,2n]上的最大值为f(x)=12f(x+2),且数列{an}的前n项和为Sn.若对于任意正整数n不等式k(Sn+1)≥2n-9恒成立,则实数k的取值范围为( )an(n∈N*)组卷:358引用:2难度:0.4 -
2.已知{an}为正项等比数列,Sn是它的前n项和.若a1=16,且a4与a7的等差中项为
,则S5的值( )98组卷:137引用:6难度:0.7 -
3.已知x=0是函数f(x)=x(ax-tanx)的极大值点,则a的取值范围是( )
组卷:200引用:3难度:0.5 -
4.已知函数f(x)=x2-3x+5,g(x)=ax-lnx,若对∀x∈(0,e),∃x1,x2∈(0,e)且x1≠x2,使得f(x)=g(xi)(i=1,2),则实数a的取值范围是( )
组卷:825引用:14难度:0.4 -
5.已知集合A={y|y=
},B={x|y=lg(x-2x2)},则∁R(A∩B)=( )x2-1组卷:152引用:6难度:0.9 -
6.已知函数
为奇函数,则m=( )f(x)=x3+sinx(1+x)(m-x)+ex+e-x组卷:159引用:2难度:0.8 -
7.已知集合A={x|x+1≤0},B={x|x≥a},若A∪B=R,则实数a的值可以为( )
组卷:468引用:8难度:0.8
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知椭圆C的焦点在x轴上,且顺次连接四个顶点恰好构成了一个边长
为且面积为23的菱形.2
(1)求椭圆C的方程;
(2)设M(-3,0),过椭圆C右焦点F的直线l交于A、B两点,若对满足条件的任意直线l,不等式≤λ(λ∈R)恒成立,求λ的最小值.MA•MB组卷:44引用:3难度:0.4 -
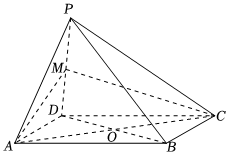 22.如图,四棱锥P-ABCD中,底面ABCD是菱形,对角线AC,BD交于点O,M为棱PD的中点,MA=MC.求证:
22.如图,四棱锥P-ABCD中,底面ABCD是菱形,对角线AC,BD交于点O,M为棱PD的中点,MA=MC.求证:
(1)PB∥平面AMC;
(2)平面PBD⊥平面AMC.组卷:813引用:2难度:0.6


