2023-2024学年上海市浦东新区建平中学高二(上)月考数学试卷(10月份)
发布:2024/9/13 18:0:9
一、填空题(1-6题每题4分,7-12题每题5分,共54分)
-
1.集合A={0,1,2},集合B={-1,0,1},则A∩B=.
组卷:34引用:3难度:0.9 -
2.不等式x(1-2x)>0的解集为
.组卷:24引用:4难度:0.7 -
3.若直线l1:ax-y+1=0与直线l2:2x-2y-1=0的倾斜角相等,则实数a=.
组卷:108引用:2难度:0.5 -
4.点(1,-1)到直线3x-4y+3=0的距离是
.组卷:237引用:6难度:0.7 -
5.两圆x2+y2-2y-3=0与x2+y2+2x=0的公共弦所在直线的方程为 .
组卷:121引用:3难度:0.7 -
6.已知双曲线
x2a2=1(a>0,b>0)的一条渐近线方程是-y2b2x-y=0,它的一个焦点为(3,0),则双曲线的标准方程为 .2组卷:91引用:5难度:0.7 -
7.双曲线
的两渐近线夹角为 .x24-y29=1组卷:58引用:2难度:0.7
三、解答题(17,18,19题每题14分,20,21题每题18分,共78分)
-
20.已知椭圆C:
=1(a>b>0)的上顶点为B2,右焦点为F2,△B2OF2为等腰直角三角形(O为坐标原点),抛物线y2=4x2a2+y2b2x的焦点恰好是该椭圆的右顶点.2
(1)求椭圆C的方程;
(2)若点B1,B2分别是椭圆的下顶点和上顶点,点P是椭圆上异与B1,B2的点,求证:直线PB1和直线PB2的斜率之积为定值.
(3)已知圆M:x2+y2=的切线l与椭圆相交于C,D两点,那么以CD为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.23组卷:66引用:3难度:0.1 -
21.已知抛物线y2=4x,顶点为O,过焦点的直线交抛物线于A,B两点.
(1)如图1所示,已知|AB|=8,求线段AB中点到y轴的距离;
(2)设点P是线段AB上的动点,顶点O关于点P的对称点为C,求四边形OACB面积的最小值;
(3)如图2所示,设D为抛物线上的一点,过D作直线DM,DN交抛物线于M,N两点,过D作直线DP,DQ交抛物线于P,Q两点,且DM⊥DN,DP⊥DQ,设线段MN与线段PQ的交点为T,求直线OT斜率的取值范围.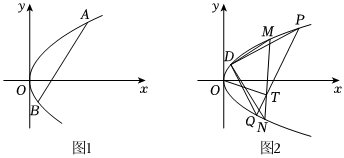 组卷:257引用:5难度:0.1
组卷:257引用:5难度:0.1


