2023年福建省厦门六中中考数学二模试卷
发布:2024/5/16 8:0:9
一、选择题。(本大题共10小题,每小题4分,共40分.每小题给出的四个选项,只有一项是符合题目要求的)
-
1.2的算术平方根是( )
组卷:96引用:5难度:0.9 -
 2.一个几何体的正视图如图所示,则这个几何体可能为( )组卷:108引用:2难度:0.7
2.一个几何体的正视图如图所示,则这个几何体可能为( )组卷:108引用:2难度:0.7 -
3.计算 a-3•a2 的结果是( )
组卷:65引用:1难度:0.5 -
4.《孙子算经》卷上说:“十圭为抄,十抄为撮,十撮为勺,十勺为合.”说明“抄、撮、勺、合”均为十进制.则十合等于( )
组卷:444引用:11难度:0.7 -
5.若方程x2+2x+m-3=0有两个不相等的实数根,则m的最大整数是( )
组卷:272引用:4难度:0.8 -
 6.如图,AB∥CD,DE=EC,∠B=35°,则∠BED=( )组卷:102引用:1难度:0.6
6.如图,AB∥CD,DE=EC,∠B=35°,则∠BED=( )组卷:102引用:1难度:0.6 -
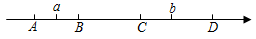 7.点a,b在数轴上的位置如图所示,且满足a+b>0,a•b<0,则原点所在的位置有可能是( )组卷:1172引用:11难度:0.8
7.点a,b在数轴上的位置如图所示,且满足a+b>0,a•b<0,则原点所在的位置有可能是( )组卷:1172引用:11难度:0.8 -
8.生物兴趣小组对某大豆杂交品种进行育苗试验,培育结果统计如下:
根据上述培育结果,下列说法正确的是( )总粒数 黄色子叶粒数 青色子叶粒数 黄色子叶粒数与青色子叶粒数的实际比率 黄色子叶粒数与青色子叶粒数的理论比率 246 187 59 3.16:1 3:1 3658 2738 920 2.98:1 3:1 7679 5781 1898 3.06:1 3:1 31213 23436 7777 3.01:1 3:1 组卷:123引用:4难度:0.7
三、解答题。(本大题有9小题,共86分)
-
24.【问题提出】
(1)如图1,在矩形ABCD中,AD=10,AB=12,点E为AD的中点,点P为矩形ABCD内以BC为直径的半圆上一点,则PE的最小值为 ;
【问题探究】
(2)如图2,在△ABC中,AD为BC边上的高,且AD=BC=4,P为△ABC内一点,当时,求PB+PC的最小值;S△PBC=12S△ABC
【问题解决】
(3)如图3,滨河学校餐厅门口有一块“疯狂四季”四边形菜园ABCD,∠ABC=∠BAD=60°,AC与BD相交于点P,且AD+BC=AB,过点A作直线BC的垂线交直线BC于点E,即AE⊥BE,BE=200米,赵老师准备在△ABP内种植当季蔬菜,边BE的中点F为菜园出入口,为了种植方便,她打算在AE边上取点M,并沿PM、MF修两条人行走道,要求人行走道的总长度尽可能小,问PM+MF的长度是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.3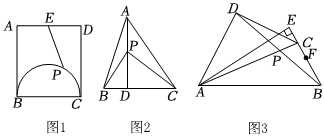 组卷:628引用:4难度:0.3
组卷:628引用:4难度:0.3 -
25.如图,已知二次函数y=-x2+bx+c的图象与x轴交于A(-1,0)、B两点,与y轴交于点C(0,3),P为x轴正半轴上一点,过点P作垂直于x轴的直线交抛物线于点D.
(1)求二次函数的表达式;
(2)如图1,若点P在B点右侧,过C垂直于DP的直线交抛物线于点H,交DP于点G,求证:PG•DG=3CG•GH;
(3)如图2,若点P在线段OB上,DP交直线BC于点E,当△CDE中有一个角与∠ABD相等,求点P的横坐标.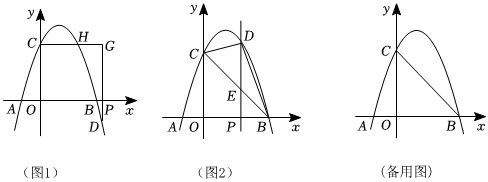 组卷:475引用:3难度:0.3
组卷:475引用:3难度:0.3


