当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省湖州五中九年级（上）期中数学试卷

发布：2024/9/4 16:0:8

一、选择题（本大题共10小题，共30分）

1．下列选项中的事件，属于随机事件的是（　　）
A．在一个只装有黑球的袋子里，摸出白球
B．两个负数相加，和为负
C．打开电视机，正在播湖州新闻
D．在一只装有黑球的袋子里，摸出黑球
组卷：5引用：2难度：0.8
解析
2．抛物线y=x²-2与y轴交点的坐标是（　　）
A．（0，2） B．（0，-2） C．（2，0） D．（-2，0）
组卷：577引用：12难度：0.9
解析
3．一个不透明袋子中装有6个黑球、3个白球，这些球除颜色外，形状、大小、质地等完全相同，随机地从这个袋子中摸出一个球，摸到白球的概率是（　　）
A．
1
9
B．
1
2
C．
2
3
D．
1
3
组卷：125引用：3难度：0.8
解析
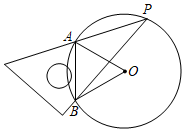4．如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，连结AO，BO，则∠AOB的度数是（　　）
A．30° B．60° C．80° D．90°
组卷：1037引用：17难度：0.5
解析
5．对于函数y=-（x-2）²+5，下列结论错误的是（　　）
A．图象顶点是（2，5） B．图象开口向下
C．图象关于直线x=2对称 D．函数最小值为5
组卷：14引用：2难度：0.6
解析
6．根据圆规作图的痕迹，可用直尺成功地找到三角形内心的是（　　）
A． B． C． D．
组卷：1020引用：30难度：0.8
解析
7．下列命题中：①任意三点确定一个圆；②同弧或等弧所对的圆心角相等；③平分弦的直径垂直于弦； ④半圆所对的弦是直径．真命题的个数是（　　）
A．4 B．3 C．2 D．1
组卷：16引用：2难度：0.5
解析
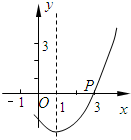8．如图，抛物线y=ax²+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a-b+c的值为（　　）
A．0 B．-1 C．1 D．2
组卷：2823引用：144难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题有8小题，共66分）

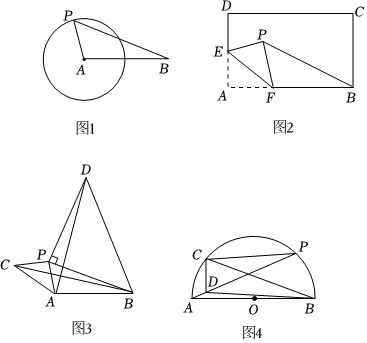23．（1）发现，如图1，在平面内，已知⊙A的半径为r,B为⊙A外一点，且AB=a.P为⊙A上一动点，连接PA，PB，易得PB的最大值为
，最小值为
．（用含a、r的代数式表示）
（2）应用，①如图2，在矩形ABCD中，AB=6，BC=4，E为AD中点，F为AB边上一动点，在平面内沿EF将△AEF翻折得到△PFF，连接PB，则PB的最小值为
．
②如图3，P为线段AB外一动点，分别以PA，PB为直角边，P为直角顶点，作等腰Rt△APC和等腰Rt△BPD，连接BC、AD．若AP=4
2
，AB=9，求AD的最大值．
（3）拓展：如图4，已知以AB为直径的半圆O，C为弧AB上一点，∠ABC=30°，P为弧BC上任意一点，CD⊥CP交AP于D，连接BD，若AB=6，则BD的最小值为
．
组卷：256引用：2难度：0.2
解析
24．如图，B（2m,0）、C（3m,0）是平面直角坐标系中两点，其中m为常数，且m＞0，E（0，n）为y轴上一动点，以BC为边在x轴上方作矩形ABCD，使AB=2BC，画射线OA，把△ADC绕点C逆时针旋转90°得△A'D'C'，连接ED'，抛物线y=ax²+bx+n（a≠0）过E、A'两点．

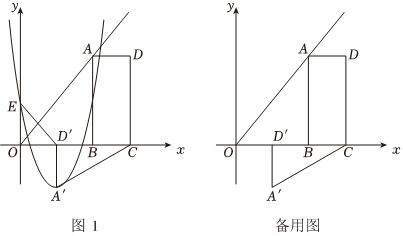
（1）填空：∠AOB=
，用m表示点A'的坐标：A'
．
（2）当抛物线的顶点为A'，抛物线与线段AB交于点P，且△A'EP与矩形ABCD的面积相等时，求m与n的关系式；
（3）若E与原点O重合，抛物线与射线OA的另一个交点为M，过M作MN垂直y轴，垂足为N：
①求a、b、m满足的关系式；
②当m为定值，抛物线与四边形ABCD有公共点，线段MN的最大值为5，请你直接写出a的取值范围．
组卷：47引用：3难度：0.5
解析