2022-2023学年江苏省连云港市灌南高级中学高二（下）第二次月考数学试卷

一、单选题（本大题共8小题，共40分。在每小题列出的选项中，选出符合题目的一项）

• 1．已知直线l经过点A（1，1，2），B（0，1，0），平面α的一个法向量为

  n

  =（-2，0，-4），则（　　）

  A．l∥α	B．l⊥α
  C．l⊂α	D．l与α相交，但不垂直
  组卷：574引用：9难度：0.8

  解析

• 2．将一枚质地均匀的骰子连续抛掷3次，则出现三个点数之和为6的概率为（　　）

  A． 1 12

  B． 5 108

  C． 1 72

  D． 7 216
  组卷：167引用：5难度：0.7

  解析

• 3．某工厂随机抽取20名工人，对他们某天生产的产品件数进行统计，数据如表，则该组数据的第75百分位数是（　　）
  

  件数	7	8	9	10	11
  人数	3	7	5	4	1

  A．8.5

  B．9

  C．9.5

  D．10
  组卷：191引用：4难度：0.7

  解析

• 4．设T=

  C

  0

  35

  +

  C

  2

  35

  +

  C

  4

  35

  +…+

  C

  34

  35

  ，则T被9除的余数是（　　）

  A．5

  B．6

  C．7

  D．8
  组卷：36引用：1难度：0.7

  解析

• 5．已知ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1，则P（ξ=1）=（　　）

  A． 1 11

  B． 4 11

  C． 6 11

  D． 7 11
  组卷：11引用：2难度：0.8

  解析

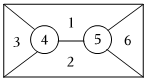• 6．现有6种不同的颜色，给图中的6个区域涂色，要求相邻区域不同色，则不同的涂色方法共有（　　）

  A．720种

  B．1440种

  C．2880种

  D．4320种
  组卷：272引用：2难度：0.7

  解析

• 7．已知随机变量ξ的分布列如表：
  

  ξ	x1	x2	x3
  P	P1	P2	P3

  其中x₂-x₁=x₃-x₂＞0．若E（ξ）＞x₂，则（　　）

  A．P1＞P2

  B．P2＜P3

  C．P2＞P3

  D．P1＜P3
  组卷：157引用：2难度：0.7

  解析

四、解答题（本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

• 21．2023年3月某学校举办了春季科技体育节，其中安排的女排赛事共有12个班级作为参赛队伍，本次比赛启用了新的排球用球MIKASA_V200W．已知这种球的质量指标ξ（单位：g）服从正态分布X～N（μ，σ²），其中u=270，σ=5．比赛赛制采取单循环方式，即每支球队进行11场比赛，最后靠积分选出最后冠军．积分规则如下（比赛采取5局3胜制）：比赛中以3：0或3：1取胜的球队积3分，负队积0分；而在比赛中以3：2取胜的球队积2分，负队积1分．9轮过后，积分榜上的前2名分别为1班排球队和2班排球队，1班排球队积26分，2班排球队积22分．第10轮1班排球队对抗3班排球队，设每局比赛1班排球队取胜的概率为p（0＜p＜1）．
  （1）令η=

  ξ

  -

  μ

  σ

  ，则η～N（0，1），且Φ（a）=P（η＜a），求Φ（-2），并证明：Φ（-2）+Φ（2）=1；
  （2）第10轮比赛中，记1班排球队3：1取胜的概率为f（p），求出f（p）的最大值点p₀，并以p₀作为p的值，解决下列问题．
  （i）在第10轮比赛中，1班排球队所得积分为X，求X的分布列；
  （ii）已知第10轮2班排球队积3分，判断1班排球队能否提前一轮夺得冠军（第10轮过后，无论最后一轮即第11轮结果如何，1班排球队积分最多）？若能，求出相应的概率；若不能，请说明理由．
  参考数据：X～N（μ，σ²），则P（μ-σ＜X≤μ+σ）≈0.6827，P（μ-2σ＜X≤μ+2σ）≈0.9545，P（μ-3σ＜X≤μ+3σ）≈0.9973．
  组卷：143引用：2难度：0.5

  解析

• 22．如图，圆台O₁O₂的轴截面为等腰梯形A₁ACC₁，AC=2AA₁=2A₁C₁=4，B为底面圆周上异于A，C的点．
  
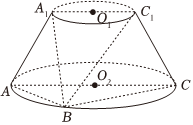
  （1）在平面BCC₁内，过C₁作一条直线与平面A₁AB平行，并说明理由；
  （2）设平面A₁AB∩平面C₁CB=l,Q∈l,BC₁与平面QAC所成角为α，当四棱锥B-A₁ACC₁的体积最大时，求sinα的取值范围．
  组卷：523引用：8难度：0.3

  解析