2023-2024学年黑龙江省牡丹江市八年级（上）期中数学试卷
发布：2024/10/3 0:0:1
一、选择题（每小题3分，满分30分）
-
1．中国文字博大精深，而且有许多是轴对称图形，在这四个文字中，不是轴对称图形的是（ ）
组卷：433引用：29难度：0.9 -
2．已知△ABC的三条边分别是a,b,c,化简|a-b+c|-|a-b-c|的结果为（ ）
组卷：127引用：3难度：0.5 -
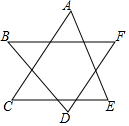3．如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（ ）组卷：146引用：4难度：0.9 -
4．下列条件中能判定△ABC≌△DEF的是（ ）
组卷：2791引用：33难度：0.7 -
5．具备下列条件的三角形中，不是直角三角形的是（ ）
组卷：136引用：5难度：0.5 -
6．一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为（ ）
组卷：869引用：7难度：0.7 -
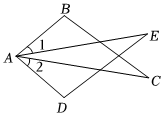7．如图，已知∠B=∠D，AB=AD，添加下列条件：①AC=AE；②∠1=∠2；③BC=DE；④∠C=∠E中的一个，能使△ABC≌△ADE的条件有（ ）组卷：16引用：1难度：0.5 -
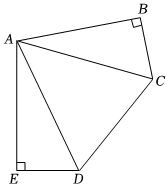8．如图，在五边形ABCDE中，∠B=∠E=90°，，AB=AE，且CD=4，AE=3，则五边形ABCDE的面积为（ ）∠CAD=12∠BAE组卷：40引用：1难度：0.9
三、解答题（满分60分）
-
24．课外兴趣小组活动时，老师提出了下面问题：
如图①，AD是△ABC的中线，若AB=3，AC=5，求AD的取值范围．
“善思小组”通过探究发现，延长AD至点E，使ED=AD，连接CE，可以证出△ADB≌△EDC，利用全等三角形的性质，可将已知的边长与AD转化到△ACE中，进而求出AD的取值范围．
从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
请你利用“善思小组”的方法思考：
（1）由已知和作图能得到△ADB≌△EDC的理由是 ；
A．SSS
B．AAS
C．HL
D．SAS
（2）求得AD的取值范围是 ；
A.3＜AD＜5
B.3≤AD≤5
C.1＜AD＜4
D.1≤AD≤4
解题时，条件中若出现“中点”或“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一三角形中．
根据上面解题方法的启发，请你解答问题．
（3）如图②，在△ABC中，AB＞AC，点D，E在BC上，点E是CD的中点，DF∥AB交AE于点F，DF=AC．
求证：AE平分∠BAC．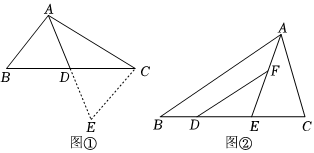
组卷：237引用：1难度：0.5 -
25．探究式学习是新课程倡导的重要学习方法，某数学兴趣小组拟做以下探究．
如图，在△ABC中，BD、CE分别是AC、AB上的高，点G在直线CE上，CG=AB，点F在直线BD上，BF=AC，FN⊥BC于点N，GM⊥BC于点M．探究线段BC，FN，GM之间的数量关系．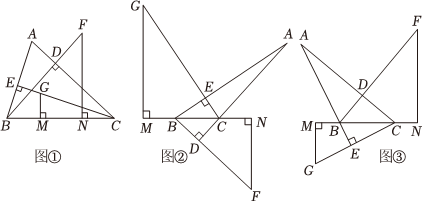
（1）如图①，当△ABC是锐角三角形时，线段BC，FN，GM之间的数量关系是 ．
“善思小组”通过探究后发现解决此问题的方法：过点A作AP⊥BC于点P，利用全等三角形的性质进而得证．请你写出证明过程．
下面是小强的部分证明过程，仔细阅读并完成相应的任务．
请你补全余下的证明过程．证明：过点A作AP⊥BC于点P．
∴∠APB=90°．
∴∠BAP+∠ABP=90°．
∵CE⊥AB，
∴∠BCE+∠ABP=90°．
∴∠BAP=∠BCE．
∵GM⊥BC，
∴∠CMG=90°．∴∠APB=∠CMG=90°．
在△APB和△CMG中，
∵∠BAP=∠GCM，
∠APB=∠CMG，AB=CG，
∴△APB≌△CMG（AAS）．
∴BP=GM．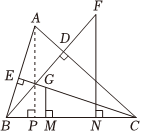
（2）通过类比、转化、猜想，探究出：当△ABC是钝角三角形，且AB＞AC时，如图②线段BC，FN，GM之间的数量关系是 ；当△ABC是钝角三角形，且AB＜AC时，如图③，线段BC，FN，GM之间的数量关系是 ．
（3）“智慧小组”继续对上述问题进行特殊化研究后，提出下面问题请你解答：
在（1）和（2）的条件下，若MN=2BC=8，CD：AD=1：3，则S△BCD=．组卷：65引用：1难度：0.4
