课外兴趣小组活动时，老师提出了下面问题：
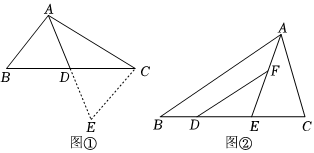
如图①，AD是△ABC的中线，若AB=3，AC=5，求AD的取值范围．
“善思小组”通过探究发现，延长AD至点E，使ED=AD，连接CE，可以证出△ADB≌△EDC，利用全等三角形的性质，可将已知的边长与AD转化到△ACE中，进而求出AD的取值范围．
从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
请你利用“善思小组”的方法思考：
（1）由已知和作图能得到△ADB≌△EDC的理由是 DD；
A．SSS
B．AAS
C．HL
D．SAS
（2）求得AD的取值范围是 CC；
A.3＜AD＜5
B.3≤AD≤5
C.1＜AD＜4
D.1≤AD≤4
解题时，条件中若出现“中点”或“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一三角形中．
根据上面解题方法的启发，请你解答问题．
（3）如图②，在△ABC中，AB＞AC，点D，E在BC上，点E是CD的中点，DF∥AB交AE于点F，DF=AC．
求证：AE平分∠BAC．
【考点】三角形综合题．
【答案】D；C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 0:0:1组卷：237引用：1难度：0.5
相似题
-
1．（1）如图1，在△ABC中，∠ACB=2∠B，CD平分∠ACB，交AB于点D，DE∥AC，交BC于点E．
①若DE=1，BD=，求BC的长；32
②试探究-ABAD是否为定值．如果是，请求出这个定值；如果不是，请说明理由．BEDE
（2）如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF=2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE∥AC，交CB的延长线于点E．记△ACD的面积为S1，△CDE的面积为S2，△BDE的面积为S3．若S1•S3=916，求cos∠CBD的值．S22
发布：2025/6/10 12:30:1组卷：4095引用：8难度：0.3 -
2．已知△ABC是边长为4的等边三角形，点D是射线BC上的动点，将AD绕点A逆时针方向旋转60°得到AE，连接DE．
（1）如图1，猜想△ADE是什么三角形？；（直接写出结果）
（2）如图2，点D在射线CB上（点C的右边）移动时，证明∠BCE+∠BAC=180°．
（3）点D在运动过程中，△DEC的周长是否存在最小值？若存在．请求出△DEC周长的最小值；若不存在，请说明理由．发布：2025/6/10 12:30:1组卷：278引用：2难度：0.1 -
3．如图，在△ABC中，AB=AC．
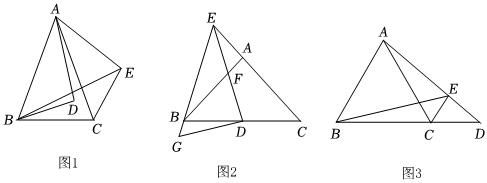
（1）如图1，在△ABC内取点D，连接AD，BD，将AD绕点A逆时针旋转至AE，∠BAC=∠DAE，连接BE，CE，∠BCE=120°，若BE=2BD=4，求BC的长；
（2）如图2，点D为BC中点，点E在CA的延长线上，连接ED交AB于点F，EF=FD，连接EB并延长至点G，连接GD，若∠BGD=60°，BF=GD，求证：GD=BG+DF；
（3）如图3，∠ABC=60°，点D在BC的延长线上，连接AD，在AD上取点E，AE=2DE，连接BE，CE，若BD=12，当CE取最小值时，直接写出△BED的面积．发布：2025/6/10 11:30:1组卷：474引用：4难度：0.2
