探究式学习是新课程倡导的重要学习方法,某数学兴趣小组拟做以下探究.
如图,在△ABC中,BD、CE分别是AC、AB上的高,点G在直线CE上,CG=AB,点F在直线BD上,BF=AC,FN⊥BC于点N,GM⊥BC于点M.探究线段BC,FN,GM之间的数量关系.
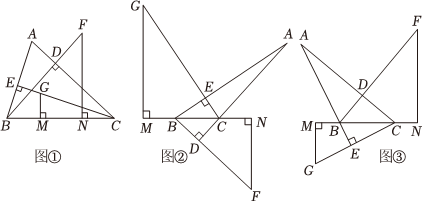
(1)如图①,当△ABC是锐角三角形时,线段BC,FN,GM之间的数量关系是 BC=GM+FNBC=GM+FN.
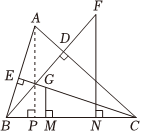
“善思小组”通过探究后发现解决此问题的方法:过点A作AP⊥BC于点P,利用全等三角形的性质进而得证.请你写出证明过程.
下面是小强的部分证明过程,仔细阅读并完成相应的任务.
| 证明:过点A作AP⊥BC于点P. ∴∠APB=90°. ∴∠BAP+∠ABP=90°. ∵CE⊥AB, ∴∠BCE+∠ABP=90°. ∴∠BAP=∠BCE. ∵GM⊥BC, ∴∠CMG=90°. |
∴∠APB=∠CMG=90°. 在△APB和△CMG中, ∵∠BAP=∠GCM, ∠APB=∠CMG,AB=CG, ∴△APB≌△CMG(AAS). ∴BP=GM. |
|
(2)通过类比、转化、猜想,探究出:当△ABC是钝角三角形,且AB>AC时,如图②线段BC,FN,GM之间的数量关系是
BC=GM-FN
BC=GM-FN
;当△ABC是钝角三角形,且AB<AC时,如图③,线段BC,FN,GM之间的数量关系是 BC=FN-GM
BC=FN-GM
.(3)“智慧小组”继续对上述问题进行特殊化研究后,提出下面问题请你解答:
在(1)和(2)的条件下,若MN=2BC=8,CD:AD=1:3,则S△BCD=
3或6
3或6
.【考点】三角形综合题.
【答案】BC=GM+FN;BC=GM-FN;BC=FN-GM;3或6
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/3 0:0:1组卷:65引用:1难度:0.4
相似题
-
1.在Rt△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若BM⊥AN于点M,CN⊥AN于点N,求证:CN=AM.
(2)如图2,点A,B分别在y轴和x轴上,直角边AC交x轴于点D,斜边BC交y轴于点E,若C点的横坐标为-2,直接写出点A的坐标.
(3)如图3,若B(-5,0),以OA为直角边在第一象限作Rt△AOD,且AD=AO,连接CD交y轴于P,问当点A在y轴的正半轴上运动时,AP的长度是否变化?若变化,请说明理由,若不变化,求出AP的长度.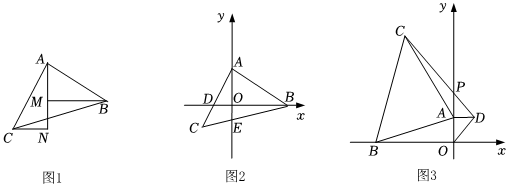 发布:2025/6/13 3:30:1组卷:40引用:1难度:0.3
发布:2025/6/13 3:30:1组卷:40引用:1难度:0.3 -
2.如图1,已知,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D在AB上且
,点P,Q分别从点D,B出发沿线段DB,BC向终点B,C匀速移动,P,Q两点同时出发,同时到达终点.设BQ=x,AP=y.BD=154
(1)求AD的值.
(2)求y关于x的函数表达式.
(3)如图2,过点P作PE⊥AC于点E,连结PQ,EQ.
①当△PEQ为等腰三角形时,求x的值.
②过D作DF⊥BC于点F,作点F关于EQ的对称点F',当点F'落在△PQB的内部(不包括边界)时,则x的取值范围为 .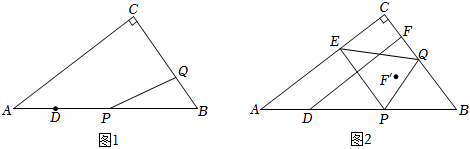 发布:2025/6/13 1:30:1组卷:84引用:3难度:0.1
发布:2025/6/13 1:30:1组卷:84引用:3难度:0.1 -
3.在等腰△ABC中,AB=AC,∠BAC=120°,D、E、F分别为线段BC、AB、AC上的点,∠AEF=∠CAD,AD交EF于点G.
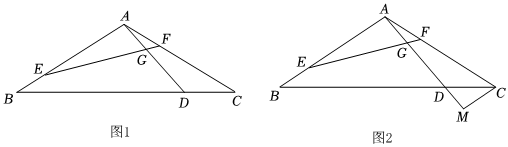
(1)如图1,求∠AGE的度数;
(2)如图2,已知BE=AF,点M在AD的延长线上,AM=EF,连接CM.
①求证:CM∥AB;②若,直接写出ADEF=45的值为 .CMAB发布:2025/6/13 1:30:1组卷:64引用:2难度:0.1


