2023-2024学年浙江省温州十二中、十四中集团校九年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，共30分）

• 1．一个袋子中有2只红球，随机取出1只球是黑球是（　　）

  A．不可能事件	B．必然事件
  C．随机事件	D．以上说法均错
  组卷：29引用：2难度：0.7

  解析

• 2．抛物线y=x²-4与y轴的交点坐标是（　　）

  A．（0，-4）

  B．（-4，0）

  C．（2，0）

  D．（0，2）
  组卷：736引用：10难度：0.9

  解析

• 3．将函数y=-x²的图象向上平移2个单位，所得图象对应的函数表达式是（　　）

  A．y=-x2+2

  B．y=-x2-2

  C．y=-（x+2）2

  D．y=-（x-2）2
  组卷：217引用：4难度：0.6

  解析

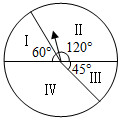• 4．如图是一个游戏转盘，自由转动转盘，当转盘停止转动后，指针落在数字“Ⅱ”所示区域内的概率是（　　）

  A． 1 3

  B． 1 4

  C． 1 6

  D． 1 8
  组卷：1829引用：41难度：0.8

  解析

• 5．将二次函数y=x²-2x+3化为y=（x+m）²+h的形式，结果为（　　）

  A．y=（x-1）2+4

  B．y=（x+1）2+4

  C．y=（x-1）2+2

  D．y=（x+1）2+2
  组卷：759引用：12难度：0.9

  解析

• 6．某校即将举行田径运动会，“体育达人”小明从“跳高”“跳远”“100米”“400米”四个项目中，随机选择两项，则他选择“100米”与“400米”两个项目的概率是（　　）

  A． 1 2

  B． 1 4

  C． 1 6

  D． 1 12
  组卷：1358引用：13难度：0.7

  解析

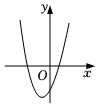• 7．如图，关于抛物线y=ax²+bx+c,下列说法正确的是（　　）

  A．a＜0

  B．b＜0

  C．c＜0

  D．b2-4ac=0
  组卷：43引用：2难度：0.5

  解析

三、解答题（共7小题，共66分，解答需写出必要的文字说明或演算步骤）

• 22．根据以下素材，探索完成任务．
  

  素材1	如图，某小区的景观池中安装一雕塑OA，OA=2米，在点A处安装喷水装置，喷出两股水流，两股水流可以抽象为平面直角坐标系中的两条抛物线（图中的C1，C2）的部分图象，两条抛物线的形状相同且顶点的纵坐标相同，且经测算发现抛物线C1的最高点（顶点）B距离水池面2.5米，且与OA的水平距离为2米．
  素材2	小明同学打算操控微型无人机在C1之间飞行，为了无人机的安全，要求无人机在竖直方向上的活动范围不小于0.5米．
  任务1	求抛物线C1的解析式；
  任务2	求抛物线C2与x轴的交点D的坐标；
  任务3	设无人机与OA的水平距离为m,求m的取值范围．
  组卷：202引用：1难度：0.6

  解析

• 23．如图1，抛物线与x轴交于A、B两点，与y轴交于点C（0，3），且OB=OC=3AO．直线y=x+1与抛物线交于A、D两点，与y轴交于点E，点Q是抛物线的顶点．
  
  （1）求该抛物线的解析式及顶点Q的坐标．
  （2）连结CQ，判断线段CQ与线段AE有何关系，请说明理由．
  （3）如图2，若点P是直线AD上方的抛物线上的一动点，设点P的横坐标为m.
  ①连结PA、PD，当m为何值时，S_△PAD=

  1

  2

  S_△DAB．
  ②在直线AD上是否存在一点H使△PQH为等腰直角三角形，若存在请求出m的值，若不存在请说明理由．
  组卷：398引用：3难度：0.2

  解析