2022-2023学年江苏省宿迁市泗阳县九年级（上）期中数学试卷
发布：2024/7/16 8:0:9
一、选择题（本大题共10小题，每题3分，共30分，每小题只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置）
-
1．一元二次方程x2+2x+1=0的解是（ ）
组卷：1274引用：24难度：0.9 -
2．已知⊙O的半径为6cm,点P在⊙O内，则OP的长（ ）
组卷：255引用：3难度：0.9 -
3．用配方法解一元二次方程x2-4x-1=0时，配方得（ ）
组卷：686引用：11难度：0.7 -
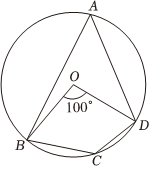4．如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为（ ）组卷：11330引用：116难度：0.7 -
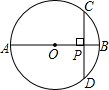5．如图，AB是⊙O的直径，弦CD⊥AB，垂足为P．若CD=8，OP=3，则⊙O的半径为（ ）组卷：786引用：78难度：0.9 -
6．我县近几年的初中毕业生出现持续增长趋势，2020年的初三毕业生大约15000人，2022年的初三毕业生大约16500人．若设这两年的平均增长率为x,则x应满足的方程是（ ）
组卷：20引用：1难度：0.6 -
7．已知直角三角形的两条直角边长分别为6和8，它的内切圆半径是（ ）
组卷：375引用：6难度：0.9 -
8．下列命题中，正确的是（ ）
组卷：135引用：3难度：0.9 -
9．已知x=a是一元二次方程x2-x-1=0较大的根，则下面对a的估计正确的是（ ）
组卷：140引用：2难度：0.5
三、解答题（共10小题，共96分.解答时应写出必要的步骤、过程或文字说明.）
-
27．我们知道到三角形三个顶点距离相等的点是三角形的外心．在三角形内部到三边距离相等的点是三角形的内心．由此，我们可以引入如下新的概念：
定义1：到三角形两个顶点距离相等的点叫做这个三角形的准外心，如图①，PA=PB，点P叫做△ABC的准外心，也可以称作△ABC边AB上的准外心．
定义2：到三角形的内角两边距离相等的点叫做这个三角形的准内心，如图②，QD⊥AB，QE⊥AC，且QD=QE，则点Q叫做△ABC的准内心，也可以称作△ABC边AB和AC上的准内心．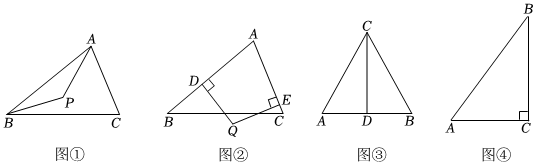
应用：
（1）如图③，CD为等边三角形ABC的高，准外心P在高CD上，且，则∠APB=°．PD=12AB
（2）如图④，在Rt△ABC中，∠C=90°，AC=3，AB=5．
①若点M是△ABC的准内心，且M在边BC上，求CM的长；
②若点N是△ABC的准外心，且是△ABC边CA和CB上的准内心，求CN的值．组卷：144引用：1难度：0.2 -
28．如图①，在平面直角坐标系中，点A坐标为（0，-1），点B坐标为B（4，-1），点C坐标为（0，2），直线y=1与y轴相交于点D，与线段BC相交于点E，P为直线DE上一点，以P为圆心，PD长为半径作⊙P．
（1）当点P坐标为（-2，1）时，则⊙P与直线AB的位置关系为 ；
（2）当⊙P与△ABC三边共有三个公共点时，则点P的横坐标x应满足的条件为 ；
（3）如图②，当点P在第二象限时，且⊙P与x轴交于M、N两点（M在N的左边），以MN为对称轴，将MN下方的OP翻折到MN的上方，作⊙P的直径NQ交OP于点Q．
①如图③，当翻折后的弧MN经过圆心P时，则点P的坐标为 ；
②当翻折后的弧MN把直径NQ分成3：2两段时，求点P的坐标．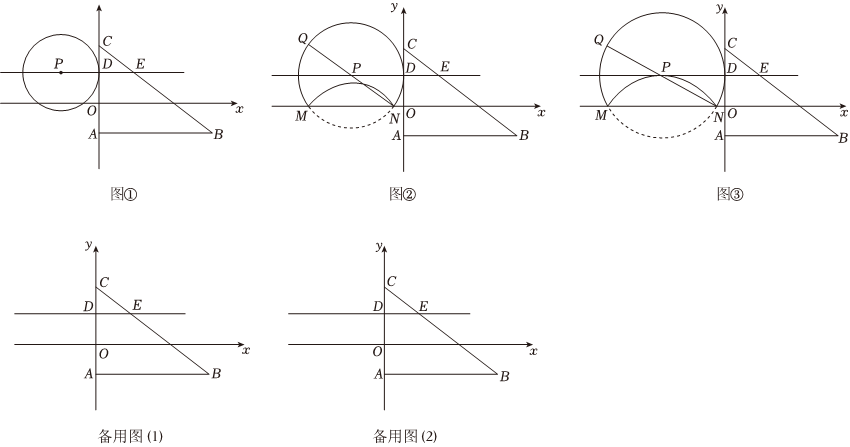
组卷：145引用：3难度：0.5
