2022-2023学年浙江省强基联盟高一(下)统测数学试卷(5月份)
发布:2024/7/1 8:0:9
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
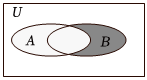 1.设全集U=R,A={x|-1≤x≤1},B={x∈N|x-3≤0},则图中阴影部分对应的集合是( )组卷:75引用:6难度:0.7
1.设全集U=R,A={x|-1≤x≤1},B={x∈N|x-3≤0},则图中阴影部分对应的集合是( )组卷:75引用:6难度:0.7 -
2.已知
(其中i为虚数单位),则z=( )iz=1+i组卷:33引用:2难度:0.8 -
3.下列说法错误的是( )
组卷:109引用:4难度:0.7 -
4.设M是平行四边形ABCD的对角线的交点,则
=( )2MA+3MB+3MC+2MD组卷:688引用:4难度:0.7 -
5.若{a∈R|∀x∈R,
={x∈R|x²-x+c<0,c∈R},则c=( )x2+ax+a4+12>0}={x∈R|x2-x+c<0,c∈R}组卷:39引用:1难度:0.6 -
6.若
,则( )a=sin5,b=log32,c=ln2,d=e0.001组卷:28引用:2难度:0.6 -
7.已知函数f(x)=2sin2ωx(ω>0),将函数y=f(x)的图象向左平移
个单位长度后得到函数y=g(x)的图象,若关于x的方程π12ω在g(x)=3上有且仅有三个不相等的实根,则实数ω的取值范围是( )[0,7π12]组卷:71引用:2难度:0.6
四、解答题:第17题10分,18~22题每题12分,共70分.解答应写出文字说明、证明过程或演算步骤.
-
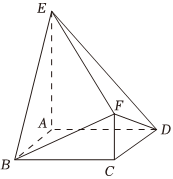 21.如图.在多面体ABCDEF中,平面EAB⊥平面ABCD,平面EAD⊥平面ABCD,ABCD是菱形,∠ABC=60°,AB=2,FC∥EA,EA=3,FC=1.
21.如图.在多面体ABCDEF中,平面EAB⊥平面ABCD,平面EAD⊥平面ABCD,ABCD是菱形,∠ABC=60°,AB=2,FC∥EA,EA=3,FC=1.
(1)证明:FC⊥平面ABCD;
(2)求二面角B-EF-D的平面角的余弦值.组卷:125引用:1难度:0.6 -
22.已知函数
,其中a>0.f(x)=2asin2x+(a-1)(sinx+cosx)+2a-8,x∈[-π2,0]
(1)当a=2时,求f(x)的值域;
(2)若对任意+1,求实数a的取值范围.x1,x2∈[-π2,0],|f(x1)-f(x2)|≤a2组卷:49引用:2难度:0.4


