2022-2023学年河南省南阳市桐柏第一高级中学高一（下）期末数学试卷

一、选择题（共8小题，每小题5分，共40分）

• 1．复数z=1-i（i为虚数单位），则

  z

  对应复平面内的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：9引用：2难度：0.7

  解析

• 2．“有两个面平行，其余各面都是平行四边形”是“几何体为棱柱”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要
  组卷：66引用：4难度：0.7

  解析

• 3．定义向量

  a

  ，

  b

  运算

  a

  ×

  b

  结果是一个向量，它的模是

  |

  a

  ×

  b

  |

  =

  |

  a

  |

  |

  b

  |

  sin

  〈

  a

  ，

  b

  〉

  ，其中

  〈

  a

  ，

  b

  〉

  表示向量

  a

  ，

  b

  的夹角．已知向量

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，且

  〈

  a

  ，

  b

  〉

  =

  5

  π

  6

  ，则

  |

  a

  ×

  b

  |

  =（　　）

  A．1

  B．-1

  C． 3

  D． - 3
  组卷：16引用：1难度：0.5

  解析

• 4．已知α为锐角，

  sin

  （

  π

  4

  -

  α

  ）

  =

  -

  3

  5

  ，则sinα=（　　）

  A． 2 10

  B． 2 2 5

  C． 3 2 5

  D． 7 2 10
  组卷：242引用：3难度：0.7

  解析

• 5．要得到函数y=2cos2x的图象．只需将函数

  y

  =

  2

  sin

  （

  2

  x

  +

  π

  6

  ）

  的图象（　　）

  A．向右平移 π 3 个单位长度	B．向左平移 π 3 个单位长度
  C．向右平移 π 6 个单位长度	D．向左平移 π 6 个单位长度
  组卷：54引用：2难度：0.7

  解析

• 6．设m,n为两条直线，α，β为两个平面，下列四个命题中，正确的命题是（　　）

  A．若m⊥α，n⊥β，α⊥β，则m⊥n

  B．若m∥α，m∥β，n∥α，n∥β，则α∥β

  C．若m⊥n,α∥β，m∥α，则n⊥β

  D．若m∥α，α⊥β，n⊂β，则m⊥n
  组卷：71引用：2难度：0.6

  解析

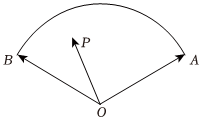• 7．如图扇形AOB所在圆的圆心角大小为

  2

  π

  3

  ，P是弧AB上任意一点，若

  OP

  =

  x

  OA

  +

  y

  OB

  ，那么2x+y的最小值是（　　）

  A．0

  B． 2 21 3

  C．1

  D． 3 3 2
  组卷：144引用：2难度：0.5

  解析

四、解答题（共6小题，共70分）

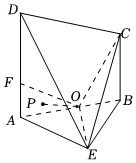• 21．如图，DA和CB都垂直于平面ABE，F是DA上一点，且CB=4，AF=2，△ABE为等腰直角三角形，且O是斜边AB的中点，CE与平面ABE所成的角为45°．
  （1）证明：FO⊥平面OCE；
  （2）求二面角F-EC-O的平面角的正切值；
  （3）若点P是平面ADE内一点，且OC⊥OP，设点P到平面ABE的距离为d₁，PA=d₂，求d₁+d₂的最小值．
  组卷：967引用：7难度：0.1

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  2

  sin

  （

  1

  2

  ωx

  ）

  cos

  （

  1

  2

  ωx

  +

  φ

  ）

  ，ω＞0，

  |

  φ

  |

  ≤

  π

  2

  ．
  （1）当ω=2，

  φ

  =

  π

  3

  时，
  ①求f（x）的单调递增区间；
  ②当

  x

  ∈

  [

  0

  ，

  π

  2

  ]

  时，关于x的方程10[f（x）]²-（10m+1）f（x）+m=0恰有4个不同的实数根，求m的取值范围．
  （2）函数g（x）=f（x）+sinφ，

  x

  =

  -

  π

  4

  是g（x）的零点，直线

  x

  =

  π

  4

  是g（x）图象的对称轴，且g（x）在

  （

  π

  18

  ，

  5

  π

  36

  ）

  上单调，求ω的最大值．
  组卷：224引用：4难度：0.5

  解析