当前位置：试卷中心 > 试卷详情

2022-2023学年北京十三中分校八年级（上）期中数学试卷

发布：2024/8/27 11:0:13

一、选择题（本题共16分，每小题2分）

1．下列运算中，结果正确的是（　　）
A．（a²）³=a⁵ B．（3a）²=6a² C．a⁶÷a²=a³ D．a²•a³=a⁵
组卷：350引用：4难度：0.9
解析
2．如图，用三角板画△ABC，BC边上的高线，下列三角板的摆放位置正确的是（　　）
A． B． C． D．
组卷：93引用：4难度：0.5
解析
3．下列各式中从左到右的变形，是因式分解的是（　　）
A．a（a+b-1）=a²+ab-a
B．a²-a-2=a（a-1）-2
C．4a²-9b²=（2a+3b）（2a-3b）
D．
2
x
+
1
=
x
（
2
+
1
x
）
组卷：41引用：1难度：0.8
解析
4．课堂上，老师组织大家用小棒摆三角形．已知三条线段的长分别是4，4，m,若它们能构成三角形，则整数m的最大值是（　　）
A．10 B．8 C．7 D．4
组卷：72引用：2难度：0.6
解析
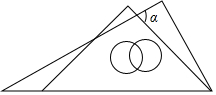5．将一副三角尺按如图所示的方式摆放，则∠α的大小为（　　）
A．85° B．75° C．65° D．60°
组卷：3878引用：58难度：0.8
解析
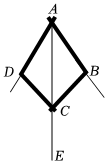6．老师上课用磁力小棒设计了一个平分角的仪器，用它可以平分一个已知角．其中AB=AD，BC=DC，将点A放在一个角的顶点，AB和AD沿着这个角的两边放下，利用全等三角形的性质就能说明射线AC是这个角的平分线．这里判定△ABC和△ADC是全等三角形的依据是（　　）
A．SSS B．ASA C．SAS D．AAS
组卷：506引用：4难度：0.7
解析
7．某中学要举行活动，现计划在教学楼之间的广场上搭建舞台．已知广场中心有一座边长为b的正方形的花坛．学生提出两个方案：
方案一：如图1，围绕花坛搭建外围为正方形的“回”字形舞台（阴影部分），舞台的面积记为S₁；
方案二：如图2，在花坛的三面搭建“凹”字形舞台（阴影部分），舞台的面积记为S₂；具体数据如图所示，则S₁与S₂的大小关系为（　　）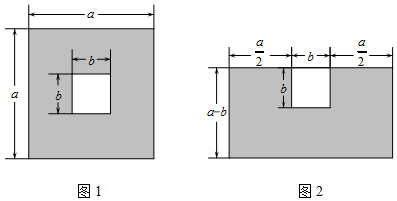
A．S₁＞S₂ B．S₁＜S₂ C．S₁=S₂ D．不能确定
组卷：66引用：1难度：0.6
解析
8．在△ABD与△ACD中，∠BAD=∠CAD，且B点，C点在AD边两侧，则不一定能使△ABD和△ACD全等的条件是（　　）
A．BD=CD B．∠B=∠C C．AB=AC D．∠BDA=∠CDA
组卷：136引用：5难度：0.7
解析

二、填空题（本题共16分，每小题2分）

9．计算：（π-1）⁰=
．
组卷：770引用：22难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共68分）；

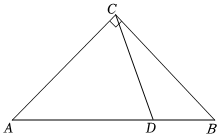27．如图，在△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点（不与点A，B重合），连接CD，过点A作AE⊥CD于E，在线段AE上截取EF=EC，连接BF交CD于G．
（1）依题意补全图形；
（2）求证：∠CAE=∠BCD；
（3）判断线段BG与GF之间的数量关系，并证明．
组卷：131引用：2难度：0.5
解析
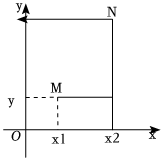28．我们知道，数轴上表示x₁x₂的两个点之间的距离可以记为d=|x₁-x₂|，类似地，在平面直角坐标系xOy.我们规定：任意两点M（x₁，y₁），N（x₂，y₂）之间的“折线距离”为d（M，N）=|x₁-x₂|+|y₁-y₂|．
例如，点P（3，9）与点Q（5，-2）之间的折线距离为d（P，Q ）=|3-5|+|9-（-2）|=2+11=13．
回答下列问题：
（1）已知点A的坐标为（2，0）
①若点B的坐标为（-3，6），则d（A，B）=

②若点C的坐标为（1，t），且d（A，C）=5，则t=

③若点D是直线y=x上的一个动点，则d（A，D）的最小值为

（2）已知O点为坐标原点，若点E（x,y）满足d（E，O）=1，请在图中画出所有满足条件的点E组成的图形．
组卷：112引用：1难度：0.7
解析