2022-2023学年吉林省长春市榆树市八号镇七年级（下）期末数学试卷

一．选择题（每题3分共24分）

• 1．若x²=4，则x的值是（　　）

  A．2

  B．±2

  C．16

  D．±16
  组卷：951引用：7难度：0.9

  解析

• 2．在平面直角坐标系中，点P（-1，x²+1）（其中x为任意有理数）一定在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：722引用：8难度：0.9

  解析

• 3．下列数中

  22

  7

  ，0.101001，

  36

  ，

  3

  ，无理数是（　　）

  A． 22 7

  B．0.101001

  C． 36

  D． 3
  组卷：13引用：2难度：0.7

  解析

• 4．不等式-2x+1＜3的解集是（　　）

  A．

  B．

  C．

  D．
  组卷：123引用：4难度：0.7

  解析

• 5．我国明代数学读本《算法统宗》一书有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托如果1托为5尺，那么索长和竿子长分别为多少尺？设索长为x尺，竿子长为y尺，可列方程组为（　　）

  A． x - y = 5 2 x - y = 5	B． x - y = 5 y - x 2 = 5
  C． x - y = 5 x - y 2 = 5	D． y - x = 5 x - y 2 = 5
  组卷：444引用：12难度：0.6

  解析

• 6．下列图标既不是轴对称图形也不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：51引用：5难度：0.8

  解析

• 7．已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（　　）

  A．53°

  B．63°

  C．73°

  D．83°
  组卷：729引用：64难度：0.9

  解析

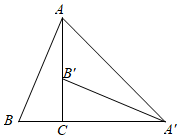• 8．如图，在△ABC中，∠ACB=90°，∠BAC=α，将△ABC绕点C顺时针旋转90°得到△A'B'C，点B的对应点B'在边AC上（不与点A，C重合），则∠AA'B'的度数为（　　）

  A．α

  B．α-45°

  C．45°-α

  D．90°-α
  组卷：2281引用：17难度：0.5

  解析

三、解答题（78分）

• 24．我们在数学学习中，经常利用“转化”的思想方法解决问题，比如，我们通过“消元的方法将二元一次方程组转化为一元一次方程，从而求解．下面我们就利用“转化”的思想方法尝试解决新的问题．
  先阅读下面的例题，再按要求完成下列问题．
  例：解不等式（x-2）（x+1）＞0．
  解：由有理数的乘法法则“两数相乘，同号得正”，得①

  x - 2 ＞ 0

  x + 1 ＞ 0

  或②

  x - 2 ＜ 0

  x + 1 ＜ 0 .

  
  解不等式组①，得x＞2．
  解不等式组②，得x＜-1．
  所以不等式（x-2）（x+1）＞0的解集为x＞2或x＜-1．
  根据例题方法解决下面问题：
  （1）解不等式（x+3）（2x-1）＜0．
  解：由有理数的乘法法则“两数相乘，异号得负”，得①

  x + 3 ＞ 0

  2 x - 1 ＜ 0

  或②

  ．
  解不等式组①，得

  ．
  解不等式组②，得

  ．
  所以不等式（x+3）（2x-1）＜0的解集为

  ．
  （2）应用：不等式：

  x

  +

  2

  x

  -

  1

  ＞

  0

  的解集为

  ．
  组卷：367引用：2难度：0.5

  解析

• 25．如图，在平面直角坐标系中，已知A（0，a），B（b,0），C（3，c）三点，其中a、b、c满足关系式：|a-2|+（b-3）²+

  c

  -

  4

  =0．
  （1）求a、b、c的值；
  （2）如果在第二象限内有一点P（m,

  1

  2

  ），请用含m的式子表示四边形ABOP的面积；
  （3）在（2）的条件下，是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍？若存在，求出所有满足条件的点P的坐标，若不存在，请说明理由．
  组卷：2112引用：5难度：0.5

  解析