当前位置：试卷中心 > 试卷详情

2023年广东省广州二中中考数学二模试卷

发布：2024/5/9 8:0:9

一、选择题（本大题共有10小题，每小题3分，共10小题，满分30分，在每题给出的四个选项中，只有一项是符合题目要求的）

1．-2023的相反数是（　　）
A．
1
2023
B．
-
1
2023
C．2023 D．3202
组卷：91引用：3难度：0.8
解析
2．奥密克戎是新型冠状病毒，其直径为140纳米（1纳米=0.000000001米）．“140纳米”用科学记数法表示为（　　）
A．1.4×10^-11米 B．0.14×10^-10米
C．1.4×10^-7米 D．0.14×10^-6米
组卷：1175引用：12难度：0.8
解析
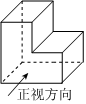3．如图所示的几何体的左视图是（　　）
A． B． C． D．
组卷：57引用：1难度：0.8
解析
4．在某学校“我的中国梦”演讲比赛中，有7名学生参加决赛，它们决赛的最终成绩各不相同，其中一名学生想知道自己能否进入前3名，不仅要知道自己的成绩，还要了解这7名学生成绩的（　　）
A．平均数 B．中位数 C．众数 D．方差
组卷：462引用：12难度：0.8
解析
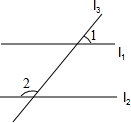5．如图，已知l₁∥l₂，∠1=50°，则∠2的度数是（　　）
A．50° B．100° C．120° D．130°
组卷：119引用：8难度：0.9
解析
6．若分式
x
2
-
9
2
x
-
6
的值为0，则x等于（　　）
A．-3 B．3 C．±3 D．0
组卷：719引用：6难度：0.9
解析
7．已知四边形ABCD是平行四边形，下列结论中错误的是（　　）
A．当∠ABC=90°时，它是矩形
B．当AB=BC时，它是菱形
C．当AC⊥BD时，它是菱形
D．当AC=BD时，它是正方形
组卷：1536引用：25难度：0.8
解析
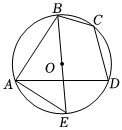8．如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE．若∠BCD=2∠BAD，则∠DAE的度数是（　　）
A．20° B．30° C．40° D．45°
组卷：692引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤）

24．如图1，AD是⊙O的直径，弦BC⊥AD，∠CAD=30°．

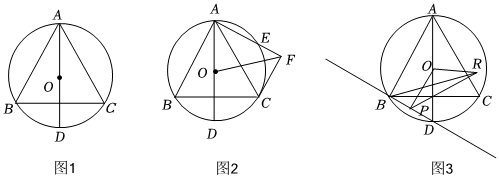
（1）求证：△ABC是等边三角形；
（2）如图2，若点E是
ˆ
AC
的中点，连接AE，过点C作CF⊥AE，垂足为F，若
CF
=
3
，求线段OF的长；
（3）若⊙O的半径为4，点P是直线BD上的动点，将点P绕点O逆时针旋转120°得点R，连接PR，BR，求PR+
3
BR的最小值．
组卷：211引用：1难度：0.3
解析
25．定义：若一个函数图象上存在横、纵坐标相等的点，则称该点为这个函数图象的“等值点”，例如，点（1，1）是函数
y
=
2
3
x
+
1
3
的图象的“等值点”．
（1）请判断函数y=x²-3x的图象上是否存在“等值点”？如果存在，求出“等值点”的坐标；如果不存在，说明理由；
（2）设函数y=x²（x＞0），y=-x+b的图象的“等值点”分别为点A，B，过点B作BC⊥x轴，垂足为C，当△ABC的面积为1时，求b的值；
（3）已知函数y₁=x²-2tx+3（t为常数）有两个“等值点”，存在函数y₂ （异于y₁），若对于任意的自变量x,都有点（x,y₁）与点（x,y₂）到点（x,x）的距离相等；当t≤x≤t+1时，都有y₂＞y₁成立，请结合图象求t的取值范围．
组卷：404引用：1难度：0.2
解析