当前位置：试卷中心 > 试卷详情

2022-2023学年江西省宜春市丰城九中高一（下）期末数学试卷

发布：2024/6/29 8:0:10

1．若a,b∈R，则“a＞b”是“a³＞b³+1”的（　　）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
组卷：128引用：3难度：0.9
解析
2．已知（3+ai）（-1+i）=-b+2i（a,b∈R，i为虚数单位），则复数
|
a
-
1
2
bi
|
=（　　）
A．2 B．
5
C．
7
D．6
组卷：62引用：3难度：0.8
解析
3．函数f（x）=ln|
1
-
x
1
+
x
|的大致图象为（　　）
A． B． C． D．
组卷：243引用：13难度：0.7
解析
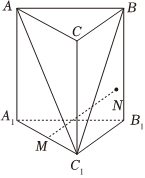4．如图，在三棱柱ABC-A₁B₁C₁中，M为A₁C₁的中点，N为侧面BCC₁B₁上的一点，且MN∥平面ABC₁，若点N的轨迹长度为2，则（　　）
A．AC₁=4 B．BC₁=4 C．AB₁=6 D．B₁C=6
组卷：308引用：8难度：0.6
解析
5．已知实数x,y满足x²+y²-4x-2y-4=0，则x-y的最大值是（　　）
A．1+
3
2
2
B．4 C．1+3
2
D．7
组卷：3706引用：16难度：0.8
解析
6．已知抛物线E：x²=4y,圆C：x²+（y-3）²=1，P为E上一点，Q为C上一点，则|PQ|的最小值为（　　）
A．2 B．
2
2
-
1
C．
2
2
D．3
组卷：185引用：8难度：0.6
解析
7．已知△ABC的内角A，B，C所对的边分别为a,b,c,满足a²+c²+ac-b²=0，则
-
tan
B
co
s
2
A
2
-
2
3
sin
B
sin
C
2
cos
C
2
的取值范围为（　　）
A．
（
3
4
，
3
2
）
B．
（
1
4
，
3
4
）
C．
（
3
4
，
1
]
D．（
3
4
，
3
3
4
）
组卷：139引用：3难度：0.5
解析

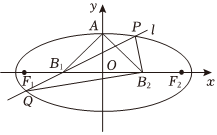21．已知椭圆的中心为原点O，长轴在x轴上，上顶点为A，左、右焦点分别为F₁，F₂，线段OF₁，OF₂的中点分别为B₁，B₂，且ΔAB₁B₂是面积为4的直角三角形．
（1）求该椭圆的标准方程；
（2）过B₁作直线l交椭圆于P，Q，PB₂⊥QB₂，求直线l的方程．
组卷：56引用：1难度：0.5
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的右焦点为F，过点F作一条直线交C于R，S两点，线段RS长度的最小值为
2
，C的离心率为
2
2
．
（1）求C的标准方程；
（2）斜率不为0的直线l与C相交于A，B两点，P（2，0），且总存在实数λ∈R，使得
PF
=λ（
PA
|
PA
|
+
PB
|
PB
|
），问：l是否过一定点？若过定点，求出该定点的坐标；若不过定点，试说明理由．
组卷：44引用：4难度：0.6
解析