已知椭圆C：x2a2+y2b2=1（a＞b＞0）的右焦点为F，过点F作一条直线交C于R，S两点，线段RS长度的最小值为2，C的离心率为22．
（1）求C的标准方程；
（2）斜率不为0的直线l与C相交于A，B两点，P（2，0），且总存在实数λ∈R，使得PF=λ（PA|PA|+PB|PB|），问：l是否过一定点？若过定点，求出该定点的坐标；若不过定点，试说明理由．
x
2
a
2
y
2
b
2
2
2
2
PF
PA
|
PA
|
PB
|
PB
|
【考点】椭圆与平面向量．
【答案】（1）+y2=1；
（2）直线恒过定点（1，0）．
x
2
2
（2）直线恒过定点（1，0）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：44引用：4难度：0.6
相似题
-
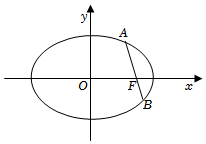1．在直角坐标系xOy中，已知椭圆的右焦点为F（1，0），过点F的直线交椭圆C于A，B两点，|AB|的最小值为C：x2a2+y2b2=1（a＞b＞0）．2
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若与A，B不共线的点P满足，求△PAB面积的取值范围．OP=λOA+（2-λ）OB发布：2024/12/29 13:30:1组卷：105引用：3难度：0.4 -
2．椭圆C：
+x2a2=1（a＞b＞0）的左、右焦点分别为F1，F2，过点F1的直线l交椭圆C于A，B两点，若|F1F2|=|AF2|，y2b2=2AF1，则椭圆C的离心率为（ ）F1B发布：2024/12/6 18:30:2组卷：762引用：6难度：0.6 -
3．已知椭圆
=1（a＞b＞0）的左、右焦点分别为F1、F2，经过F1的直线交椭圆于A，B，△ABF2的内切圆的圆心为I，若3x2a2+y2b2+4IB+5IA=IF2，则该椭圆的离心率是（ ）0发布：2024/11/28 2:30:1组卷：1231引用：13难度：0.5
