2021-2022学年四川省泸州市高一(下)期末数学试卷
发布:2024/6/25 8:0:9
一、选择题:本大题共有12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合要求的。
-
1.已知集合A={-1,0,1,2,3},B={x|-1<x<2},则A∩B=( )
组卷:121引用:16难度:0.8 -
2.已知向量
,若a=(3,-2),b=(1,x),则x=( )a∥b组卷:6引用:3难度:0.7 -
3.已知圆锥的底面半径为1,侧面展开图的圆心角为
,则该圆锥的高为( )23π组卷:13引用:3难度:0.8 -
4.在α型病毒疫情初始阶段,可以用指数函数模型I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律.指数增长率r与R0、T近似满足R0=1+rT,其中R0为病毒基本再生数,T为两代间传染所需的平均时间,有学者基于已有数据估计出R0=3.22,T=10.据此,在α型病毒疫情初始阶段,累计感染病例数增加至I(0)的4倍,至少需要( )(参考数据:ln2≈0.69)
组卷:3引用:2难度:0.6 -
5.在平行四边形ABCD中,对角线AC与BD交于点O,
+AB=λAD,则λ=( )AO组卷:98引用:6难度:0.9 -
6.已知
,则cosθ+cos(θ+π3)=1=( )cos(θ+π6)组卷:7引用:2难度:0.7 -
7.记Sn为等差数列{an}的前n项和.若a3+a5=20,S6=51,则{an}的公差为( )
组卷:3引用:2难度:0.7
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
-
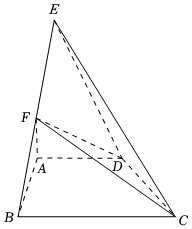 21.如图,等腰Rt△ABE与四边形ABCD所在平面互相垂直,若BF=EF,AD∥BC,AB=AE=BC=2AD.
21.如图,等腰Rt△ABE与四边形ABCD所在平面互相垂直,若BF=EF,AD∥BC,AB=AE=BC=2AD.
(Ⅰ)求证:AF∥平面CDE;
(Ⅱ)若∠ABC=90°,AB=2,求四面体CDEF的体积.组卷:25引用:2难度:0.5 -
22.已知函数f(x)=log3
.1+axx
(1)若函数f(x)的定义域为,值域为[1,2],求a的值;[18,12]
(2)若关于x的方程=1的解集中有且只有一个元素,求实数a的取值范围.f(x)log3[(a-3)x+2a-4]组卷:74引用:4难度:0.5


