2023-2024学年上海市黄浦区格致中学高二（上）期中数学试卷

一、填空题：（本题共有12个小题，1-6每小题3分，7-12每小题3分，满分42分）

• 1．i²⁰²³=

  ．
  组卷：138引用：4难度：0.8

  解析

• 2．已知平面α，直线l,点A、B，若A∈l,B∈l,且A∈α，B∈α，则l

  α （填数学符号）．
  组卷：89引用：4难度：0.9

  解析

• 3．已知空间两个角α、β，且α的两边与β的两边分别平行，若α=30°，则β的大小为

  ．
  组卷：28引用：1难度：0.8

  解析

• 4．已知正方体ABCD-A₁B₁C₁D₁的棱长为1，则异面直线AA₁与B₁D₁之间的距离是

  ．
  组卷：26引用：2难度：0.5

  解析

• 5．若

  a

  ⊥

  b

  ，

  c

  与

  a

  、

  b

  的夹角都是60°，且

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  |

  c

  |

  =

  3

  ，则

  |

  a

  +

  2

  b

  -

  c

  |

  =

  ．
  组卷：46引用：2难度：0.6

  解析

• 6．四面体ABCD的所有棱长均为2，则二面角A-BC-D的大小为

  ．
  组卷：58引用：3难度：0.5

  解析

三、解答题：（本题共有4大题，满分42分.解题时要有必要的解题步骤）

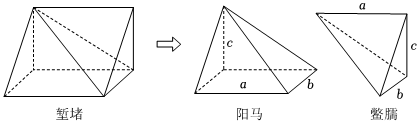
• 19．《九章算术•商功》：“斜解立方，得两堑堵．斜解堑堵，其一为阳马，一为鳖臑．阳马居二，鳖臑居一，不易之率也．合两鳖臑三而一，验之以棊，其形露矣．”刘徽注：“此术臑者，背节也，或曰半阳马，其形有似鳖肘，故以名云．中破阳马，得两鳖臑，鳖臑之起数，数同而实据半，故云六而一即得．”
  
  如图，在鳖臑ABCD中，侧棱AB⊥底面BCD；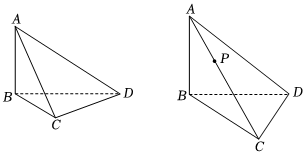
  
  （1）若AB=1，BC=2，CD=1，试求异面直线AC与BD所成角的余弦值．
  （2）若BD⊥CD，AB=BD=CD=2，点P在棱AC上运动．试求△PBD面积的最小值．
  组卷：90引用：4难度：0.4

  解析

• 20．在数列{a_n}中，

  a

  n

  =

  - 1	n = 1
  2 a n - 1 + 3	n ≥ 2

  ．在等差数列{b_n}中，前n项和为S_n，b₁=2，2b₃+S₅=28．
  （1）求数列{a_n}和{b_n}的通项公式；
  （2）设数列{c_n}满足c_n=（a_n+3b_n）cosnπ，数列{c_n}的前n项和记为T_n，试判断是否存在正整数m,使得T_m=2023？若存在，求出m的值；若不存在，说明理由．
  组卷：82引用：3难度：0.5

  解析