当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省宿迁市泗阳县高一（下）期中数学试卷

发布：2024/5/20 8:0:9

1．若3cosα+sinα=0，则tan2α=（　　）
A．
-
3
4
B．
3
4
C．
-
3
5
D．
3
8
组卷：87引用：1难度：0.7
解析
2．已知向量
a
，
b
满足|
a
|=1，
a
•
b
=-1，则
a
•（2
a
-
b
）=（　　）
A．4 B．3 C．2 D．0
组卷：1397引用：78难度：0.7
解析
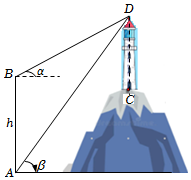3．如图，为了测量山坡上灯塔CD的高度，某人从高为h=40的楼AB的底部A处和楼顶B处分别测得仰角为β=60°，α=30°，若山坡高为a=35，则灯塔高度是（　　）
A．15 B．25 C．40 D．60
组卷：282引用：3难度：0.6
解析
4．函数y=mx²-6x+1有且只有一个零点，则实数m的值为（　　）
A．9 B．12 C．0或9 D．0或12
组卷：469引用：1难度：0.7
解析
5．在△ABC中，角A，B，C的对边分别为a,b,c,若
a
-
b
=
2
a
si
n
2
C
2
，则△ABC的形状是（　　）
A．等腰三角形或直角三角形
B．直角三角形
C．等腰三角形
D．等边三角形
组卷：101引用：6难度：0.8
解析
6．已知向量
a
=
（
1
，
1
）
，
b
=
（
3
，
y
）
，
a
+
b
与
a
平行，则
|
b
-
a
|
的值为（　　）
A．
3
B．2 C．
2
2
D．
2
3
组卷：165引用：1难度：0.8
解析
7．已知函数
f
（
x
）
=
a
-
cosx
+
3
sinx
在x∈[0，π]上有两个不同的零点，则a的取值范围为（　　）
A．[-2，1] B．[-1，1] C．
（
-
1
2
，
1
]
D．（-2，-1]
组卷：61引用：1难度：0.6
解析

21．已知△ABC满足4sinBsin（C-A）+1=4sinAsinB+cos2C，角A，B，C的对边分别是a,b,c.
（1）试问角C能否为直角？并说明理由；
（2）若△ABC为锐角三角形，且满足sinB=λsinA，求实数λ的取值范围．
组卷：21引用：1难度：0.6
解析
22．设n次多项式P_n（t）=a_ntⁿ+a_n-1t^n-1+…+a₂t²+a₁t+a₀（a_n≠0），若其满足P_n（cosx）=cosnx,则称这些多项式P_n（t）为切比雪夫多项式．例如：由cosθ=cosθ可得切比雪夫多项式P₁（x）=x,由cos2θ=2cos²θ-1可得切比雪夫多项式P₂（x）=2x²-1．
（1）若切比雪夫多项式P₃（x）=ax³+bx²+cx+d,求实数a,b,c,d的值；
（2）已知函数f（x）=8x³-6x-1在（-1，1）上有3个不同的零点，分别记为x₁，x₂，x₃，证明：x₁+x₂+x₃=0．
组卷：73引用：3难度：0.6
解析

1．若3cosα+sinα=0，则tan2α=（ ）