设n次多项式Pn（t）=antn+an-1tn-1+…+a2t2+a1t+a0（an≠0），若其满足Pn（cosx）=cosnx,则称这些多项式Pn（t）为切比雪夫多项式．例如：由cosθ=cosθ可得切比雪夫多项式P1（x）=x,由cos2θ=2cos2θ-1可得切比雪夫多项式P2（x）=2x2-1．
（1）若切比雪夫多项式P3（x）=ax3+bx2+cx+d,求实数a,b,c,d的值；
（2）已知函数f（x）=8x3-6x-1在（-1，1）上有3个不同的零点，分别记为x1，x2，x3，证明：x1+x2+x3=0．
【考点】三角函数应用．
【答案】（1）实数a，b，c，d的值分别为4，0，-3，0；
（2）证明过程见解析．
（2）证明过程见解析．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/19 8:0:9组卷：73引用：3难度：0.6
相似题
-
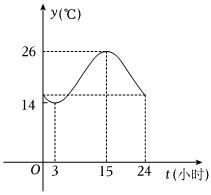1．长春某日气温y（℃）是时间t（0≤t≤24，单位：小时）的函数，该曲线可近似地看成余弦型函数y=Acos（ωt+φ）+b的图象．
（1）根据图像，试求y=Acos（ωt+φ）+b（A＞0，ω＞0，0＜φ＜π）的表达式；
（2）大数据统计显示，某种特殊商品在室外销售可获3倍于室内销售的利润，但对室外温度要求是气温不能低于23℃．根据（1）中所得模型，一个24小时营业的商家想获得最大利润，应在什么时间段（用区间表示）将该种商品放在室外销售，单日室外销售时间最长不能超过多长时间？（忽略商品搬运时间及其它非主要因素，理想状态下！）发布：2024/12/29 7:30:2组卷：45引用：4难度：0.5 -
2．筒车是我国古代发明的一种水利灌溉工具，既经济又环保．明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（图1）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都做匀速圆周运动如图2，将筒车抽象为一个半径为R的圆，设筒车按逆时针方向每旋转一周用时120秒，当t=0时，盛水筒M位于点
，经过t秒后运动到点P（x,y），点P的纵坐标满足y=f（t）=Rsin（ωt+φ）（t≥0，ω＞0，|φ|＜P0（3，-33）），则当筒车旋转100秒时，盛水筒M对应的点P的纵坐标为 ．π2
发布：2024/12/29 7:0:1组卷：127引用：3难度：0.7 -
3．某实验室白天的温度f（t）（单位：℃）随时间t（单位：h）的变化近似满足函数关系：
，t∈[6，18]．f（t）=10-2sin（π12t+π3）
（1）求实验室白天的最大温差；
（2）若要求实验室温度高于11℃，则在哪段时间实验室需要降温？发布：2024/12/29 9:0:1组卷：149引用：3难度：0.7
