2023-2024学年四川省泸州市泸县五中高二（上）月考数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知复数z满足（1+2i）z=-1+3i,则|z|=（　　）

  A． 2

  B． 3

  C．2

  D．3
  组卷：75引用：3难度：0.8

  解析

• 2．某大学数学系共有本科生1000人，其中一、二、三、四年级的人数比为4：3：2：1，要用分层抽样的方法从所有本科生中抽取一个容量为200的样本，则应抽取三年级的学生人数为（　　）

  A．80

  B．40

  C．60

  D．20
  组卷：188引用：18难度：0.9

  解析

• 3．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想可以表述为“每个大于2的偶数都可以表示为两个质数的和”，如：16=5+11．在不超过12的质数中，随机选取两个不同的数，其和为偶数的概率为（　　）

  A． 1 2

  B． 3 5

  C． 7 10

  D． 4 5
  组卷：225引用：8难度：0.8

  解析

• 4．已知

  a

  =

  （

  1

  ，-

  2

  ，

  m

  ）

  ，

  b

  =

  （

  n

  ,

  4

  ，

  6

  ）

  ，

  a

  与

  b

  共线，则m-2n=（　　）

  A．1

  B．-1

  C．2

  D．3
  组卷：24引用：2难度：0.5

  解析

• 5．已知圆锥的表面积为12πm²，且它的侧面展开图是一个半圆，则这个圆锥的体积为（　　）

  A． 6 2 π m 3

  B． 8 3 3 π m 3

  C． 2 3 3 π m 3

  D． 4 3 9 m 3
  组卷：27引用：5难度：0.8

  解析

• 6．直线

  xsinα

  +

  3

  y

  -

  b

  =

  0

  （

  a

  、

  b

  ∈

  R

  ）

  的倾斜角的取值范围是（　　）

  A．[0，π]	B． [ π 6 ， π 2 ] ∪ [ π 2 ， 5 π 6 ]
  C． [ 0 ， π 6 ] ∪ [ 5 π 6 ， π ）	D． [ π 6 ， 5 π 6 ]
  组卷：279引用：5难度：0.8

  解析

• 7．已知三棱锥S-ABC的四个顶点都在球O的球面上，且SA=BC=2，SB=AC=

  7

  ，SC=AB=

  5

  ，则球O的体积是（　　）

  A． 8 3 π

  B． 32 2 3 π

  C． 4 2 3 π

  D． 8 2 3 π
  组卷：617引用：12难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知定点A（-1，0），圆C：x²+y²-2x-2

  3

  y+3=0．
  （1）过点A向圆C引切线，求切线长；
  （2）过点A作直线l₁交圆C于P、Q，且

  AP

  =

  PQ

  ，求直线l₁的斜率k；
  （3）定点M，N在直线l₂：x=1上，对于圆C上任意一点R都满足RN=

  3

  RM，试求M，N两点的坐标．
  组卷：430引用：3难度：0.5

  解析

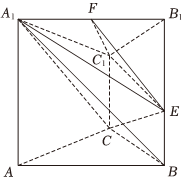• 22．如图所示，CC₁⊥平面ABC，平面ABB₁A₁⊥平面ABC，四边形ABB₁A₁⊥为正方形，∠ABC=60°，BC=CC₁=

  1

  2

  AB

  =

  2

  ，点E在棱BB₁上．
  （1）若F为A₁B₁的中点E为BB₁的中点，证明：平面EC₁F∥平面A₁CB；
  （2）设

  BE

  =

  λ

  B

  B

  1

  ，是否存在λ，使得平面A₁EC₁⊥平面A₁EC？若存在，求出λ的值；若不存在，说明理由．
  组卷：17引用：1难度：0.5

  解析