2022-2023学年北京八十中高一(下)期中数学试卷
发布:2024/6/25 8:0:9
一、选择题共10小题,每小题4分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项。
-
1.在复平面内,复数2-i对应的点在( )
组卷:118引用:3难度:0.9 -
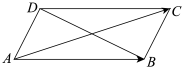 2.如图,在平行四边形ABCD中,=( )AC-AB组卷:1550引用:6难度:0.9
2.如图,在平行四边形ABCD中,=( )AC-AB组卷:1550引用:6难度:0.9 -
3.已知长方体的长、宽、高分别为5,4,3,那么该长方体的表面积为( )
组卷:285引用:4难度:0.8 -
4.已知向量
=(-1,2),a=(2,m),若b∥a,则m=( )b组卷:226引用:7难度:0.9 -
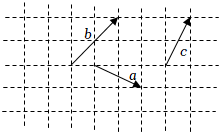 5.已知向量在正方形网格中的位置,若网格纸上小正方形的边长为1,如图所示.则a,b,c=( )(2a+b)•c组卷:233引用:7难度:0.9
5.已知向量在正方形网格中的位置,若网格纸上小正方形的边长为1,如图所示.则a,b,c=( )(2a+b)•c组卷:233引用:7难度:0.9 -
6.已知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的侧面积之比为( )
组卷:707引用:10难度:0.6 -
7.“直线l与平面α平行”是“直线l与平面α内无数条直线平行”的( )
组卷:154引用:3难度:0.7
三、解答题共6小题,共85分,某答应写出文学说明、演算步骤或证明过程。
-
 20.某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
20.某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
根据上述数据描成的曲线如图所示,经拟合,该曲线可近似地看成正弦函数y=Asinωt+b的图象.t(小时) 0 3 6 9 12 15 18 21 24 y(米) 10.0 13.0 9.9 7.0 10.0 13.0 10.1 7.0 10.0
(1)试根据数据表和曲线,求出y=Asinωt+b的表达式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间?(忽略离港所用的时间)组卷:373引用:15难度:0.3 -
21.在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)A(n):A1,A2,A3,…,An与B(n):B1,B2,B3,…,Bn,其中n≥3,若同时满足:
①两点列的起点和终点分别相同;
②线段AiAi+1⊥BiBi+1,其中i=1,2,3,…,n-1,则称A(n)与B(n)互为正交点列.
(Ⅰ)求A(3):A1(0,2),A2(3,0),A3(5,2)的正交点列B(3);
(Ⅱ)判断A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)是否存在正交点列B(4)?并说明理由;
(Ⅲ)∀n≥5,n∈N,是否都存在无正交点列的有序整点列A(n)?并证明你的结论.组卷:189引用:3难度:0.1


