当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省武汉市部分重点中学六校联考高一（下）期末数学试卷

发布：2024/6/13 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设i为虚数单位，复数z满足（1+i）z=-1+2i,则
z
•
z
为（　　）
A．
10
2
B．5 C．2 D．
5
2
组卷：152引用：5难度：0.9
解析
2．从小到大排列的数据1，2，3，x,4，5，6，7，8，y,9，10的下四分位数为（　　）
A．3 B．
3
+
x
2
C．8 D．
8
+
y
2
组卷：99引用：4难度：0.7
解析
3．已知平面向量
a
=（1，2），
b
=（3，4），那么
b
在
a
上的投影向量的坐标是（　　）
A．（
11
5
5
，
2
5
5
） B．（
5
5
，
2
5
5
） C．（
11
5
，
22
5
） D．（
5
，2
5
）
组卷：117引用：2难度：0.7
解析
4．圆台的上、下底面半径分别是1和5，且圆台的母线长为5，则该圆台的体积是（　　）
A．30π B．31π C．32π D．33π
组卷：121引用：2难度：0.8
解析
5．在边长为4的正方形ABCD中，动圆Q的半径为1、圆心在线段CD（含端点）上运动，点P是圆Q上及其内部的动点，则
AP
•
AB
的取值范围是（　　）
A．[-4，20] B．[-1，5] C．[0，20] D．[4，20]
组卷：83引用：2难度：0.6
解析
6．某校高三（1）班（45人）和高三（2）班（30人）进行比赛，按照分层抽样的方法从两个班共抽取10名同学，相关统计情况如下：高三（1）班答对题目的平均数为1，方差为1；高三（2）班答对题目的平均数为1.5，方差为0.35，则这10人答对题目的方差为（　　）
A．0.61 B．0.675 C．0.74 D．0.8
组卷：256引用：8难度：0.7
解析
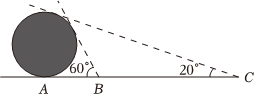7．某数学兴趣小组要测量一个球体建筑物的高度，已知点A是球体建筑物与水平地面的接触点（切点），地面上B，C两点与点A在同一条直线上，且在点A的同侧．若小明同学在B，C处分别测得球体建筑物的最大仰角为60°和20°，且BC=a米，则该球体建筑物的高度为（　　）米．
A．
a
4
cos
10
°
B．
a
2
cos
10
°
C．
asin
10
°
2
sin
40
°
D．
asin
10
°
sin
40
°
组卷：144引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

21．在△ABC中，角A，B，C所对的边分别是a,b,c,且满足
si
n
2
C
-
si
n
2
a
=
1
2
si
n
2
B
．
（1）当tanA=2时，求tanC的值；
（2）当a=2，且C-A取得最大值时，求△ABC的面积．
组卷：115引用：3难度：0.5
解析
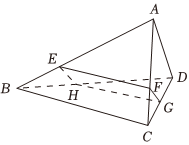22．如图，在四面体ABCD中，△ABC是边长为2的等边三角形，△DBC为直角三角形，其中D为直角顶点，∠DCB=60°．E、F，G、H分别是线段AB、AC、CD、DB上的动点，且四边形EFGH为平行四边形．
（1）当二面角A-BC-D从0°增加到90°的过程中，求线段DA在平面BCD上的投影所扫过的平面区域的面积；
（2）设
λ
=
AE
AB
，λ∈（0，1），且△ACD是以CD为底的等腰三角形，当λ为何值时，多面体ADEFGH的体积恰好为
1
4
．
组卷：71引用：2难度：0.4
解析