当前位置：试卷中心 > 试卷详情

2023年安徽省安庆市桐城中学高考数学二模试卷

发布：2024/5/17 8:0:8

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数
2
1
-
3
i
与下列复数相等的是（　　）
A．
cos
（
-
π
3
）
+
isin
（
-
π
3
）
B．
cos
（
-
π
3
）
+
isin
（
-
4
π
3
）
C．
3
2
+
1
2
i
D．
-
1
-
3
i
组卷：89引用：4难度：0.8
解析
2．已知集合M={x|x²-3x＜0}，N={x|log₂x＜4}，且全集U=[-1，20]，则U=（　　）
A．M∩（∁_UN） B．N∩（∁_UM） C．M∪（∁_UN） D．N∪（∁_UM）
组卷：152引用：6难度：0.7
解析
3．已知非零向量
a
，
b
满足
|
a
+
b
|
=
|
a
|
-
|
b
|
，则（　　）
A．
|
a
+
b
|
＞
|
b
|
B．
|
a
-
b
|
＜
|
a
|
C．
|
a
+
b
|
＞
|
a
-
b
|
D．
（
a
+
b
）
•
（
a
-
b
）
≥
0
组卷：134引用：3难度：0.7
解析
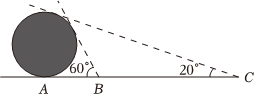4．古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作，也为地图学提供了数学基础．现根据刘徽的《重差》测量一个球体建筑物的高度，已知点A是球体建筑物与水平地面的接触点（切点），地面上B，C两点与点A在同一条直线上，且在点A的同侧．若在B，C处分别测得球体建筑物的最大仰角为60°和20°，且BC=100m,则该球体建筑物的高度约为（　　）（cos10°≈0.985）
A．49.25 m B．50.76 m C．56.74 m D．58.60 m
组卷：746引用：25难度：0.5
解析
5．法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”．他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆，这个圆称为该椭圆的蒙日圆．若椭圆Γ：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的蒙日圆为C：x²+y²=3b²，则椭圆Γ的离心率为（　　）
A．
1
3
B．
1
2
C．
3
2
D．
2
2
组卷：231引用：4难度：0.7
解析
6．已知
sinαsin
（
π
3
-
α
）
=
3
cosαsin
（
α
+
π
6
）
，则
sin
（
2
α
+
π
6
）
=（　　）
A．-1 B．
-
3
2
C．
1
2
D．
3
2
组卷：356引用：3难度：0.5
解析
7．阅读下段文字：“已知
2
为无理数，若
（
2
）
2
为有理数，则存在无理数
a
=
b
=
2
，使得a^b为有理数；若
（
2
）
2
为无理数，则取无理数
a
=
（
2
）
2
，
b
=
2
，此时
a
b
=
（
（
2
）
2
）
2
=
（
2
）
2
•
2
=
（
2
）
2
=
2
为有理数．”依据这段文字可以证明的结论是（　　）
A．
（
2
）
2
是有理数
B．
（
2
）
2
是无理数
C．存在无理数a,b,使得a^b为有理数
D．对任意无理数a,b,都有a^b为无理数
组卷：76引用：7难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共7小题，共70分。解答应写出文字说明、证明过程或演算步骤。

22．已知函数f（x）=x+1-2a e^x，x∈R．
（1）讨论函数f（x）的单调性；
（2）设函数f（x）有两个不同的零点x₁，x₂，且x₁＜x₂.若不等式x₁+λx₂＞0恒成立，求正实数λ的取值范围．
组卷：72引用：2难度：0.4
解析
23．已知双曲线C上的所有点构成集合P={（x,y）|ax²-by²=1（a＞0，b＞0）}和集合Q={（x,y）|0＜ax²-by²＜1（a＞0，b＞0）}，坐标平面内任意点N（x₀，y₀），直线l：ax₀x-by₀y=1称为点N关于双曲线C的“相关直线”．
（1）若N∈P，判断直线l与双曲线C的位置关系，并说明理由；
（2）若直线l与双曲线C的一支有2个交点，求证：N∈Q；
（3）若点N∈Q，点M在直线l上，直线MN交双曲线C于A，B，求证：
|
MA
|
|
AN
|
=
|
MB
|
|
BN
|
．
组卷：216引用：6难度：0.3
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． cos （ - π 3 ） + isin （ - π 3 ）	B． cos （ - π 3 ） + isin （ - 4 π 3 ）
C． 3 2 + 1 2 i	D． - 1 - 3 i

A． \| a + b \| ＞ \| b \|	B． \| a - b \| ＜ \| a \|
C． \| a + b \| ＞ \| a - b \|	D．（ a + b ） • （ a - b ） ≥ 0

2023年安徽省安庆市桐城中学高考数学二模试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数21-3i与下列复数相等的是（ ）

2．已知集合M={x|x2-3x＜0}，N={x|log2x＜4}，且全集U=[-1，20]，则U=（ ）

3．已知非零向量a，b满足|a+b|=|a|-|b|，则（ ）

6．已知sinαsin（π3-α）=3cosαsin（α+π6），则sin（2α+π6）=（ ）

四、解答题：本题共7小题，共70分。解答应写出文字说明、证明过程或演算步骤。

22．已知函数f（x）=x+1-2a ex，x∈R．（1）讨论函数f（x）的单调性；（2）设函数f（x）有两个不同的零点x1，x2，且x1＜x2.若不等式x1+λx2＞0恒成立，求正实数λ的取值范围．

1．复数
2
1
-
3
i
与下列复数相等的是（　　）

2．已知集合M={x|x²-3x＜0}，N={x|log₂x＜4}，且全集U=[-1，20]，则U=（　　）

3．已知非零向量
a
，
b
满足
|
a
+
b
|
=
|
a
|
-
|
b
|
，则（　　）

6．已知
sinαsin
（
π
3
-
α
）
=
3
cosαsin
（
α
+
π
6
）
，则
sin
（
2
α
+
π
6
）
=（　　）

22．已知函数f（x）=x+1-2a e^x，x∈R．
（1）讨论函数f（x）的单调性；
（2）设函数f（x）有两个不同的零点x₁，x₂，且x₁＜x₂.若不等式x₁+λx₂＞0恒成立，求正实数λ的取值范围．