2021-2022学年贵州省遵义市新蒲新区高二（上）期中数学试卷

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．点A（3，-2，4）关于点（0，1，-3）的对称点的坐标是（　　）

  A．（-3，4，-10）	B．（-3，2，-4）
  C．（ 3 2 ，- 1 2 ， 1 2 ）	D．（6，-5，11）
  组卷：244引用：13难度：0.9

  解析

• 2．直线

  x

  +

  3

  y

  +

  1

  =

  0

  的倾斜角为θ，则sinθ的值为（　　）

  A． 1 2

  B． 3 2

  C． 3 3

  D． - 3 3
  组卷：10引用：2难度：0.8

  解析

• 3．已知等腰梯形ABCD，现绕着它的较长底CD所在的直线旋转一周，所得的几何体为（　　）

  A．一个圆台、两个圆锥	B．一个圆柱、两个圆锥
  C．两个圆台、一个圆柱	D．两个圆柱、一个圆台
  组卷：170引用：8难度：0.7

  解析

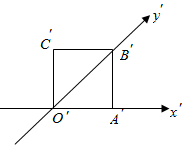• 4．如图，正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图，则原图的周长是（　　）

  A．8cm

  B．6cm

  C．2（1+ 3 ）cm

  D．2（1+ 2 ）cm
  组卷：856引用：16难度：0.9

  解析

• 5．若直线l过点（0，7），且与圆x²+y²-6x-6y+9=0相切，则直线l的方程为（　　）

  A．7x+24y-168=0	B．7x-24y-168=0
  C．x=0或7x-24y-168=0	D．x=0或7x+24y-168=0
  组卷：79引用：2难度：0.6

  解析

• 6．已知圆O₁：（x-1）²+（y+2）²=9，圆O₂：x²+y²+4x+2y-11=0，则这两个圆的位置关系为（　　）

  A．外离

  B．外切

  C．相交

  D．内含
  组卷：129引用：15难度：0.7

  解析

• 7．设m,n为两个不同的直线，α，β为两个不同的平面，则下列说法中不正确的是（　　）

  A．若m∥n,n⊥β，m⊂α，则α⊥β

  B．当m与α平行时，若m与n不平行，则n与α不平行

  C．若α⊥β，点P∈α，点P∈a,a⊥β，则a⊂α

  D．若m⊂β，α∥β，则m∥α
  组卷：42引用：2难度：0.7

  解析

三、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

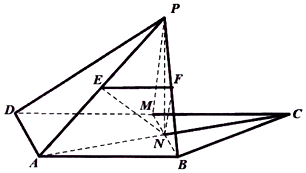• 21．如图，已知等腰梯形ABCD中，AB∥CD，AD=AB=

  1

  2

  CD，M是CD的中点，N是AC与BM的交点，将△BCM沿BM向上翻折成△BPM，使平面BPM⊥平面ABMD，E、F分别为PA、PB的中点．
  （Ⅰ）求证：平面EFN∥平面PDM；
  （Ⅱ）求直线EF与平面PAD所成角的余弦值．
  组卷：63引用：2难度：0.4

  解析

• 22．已知点P（2，0）及圆C：x²+y²-6x+4y+4=0．
  （1）设过P直线l₁与圆C交于M、N两点，当|MN|=4时，求以MN为直径的圆的方程；
  （2）设直线ax-y+1=0与圆C交于A，B两点，是否存在实数a,使得过点P（2，0）的直线l₂垂直平分弦AB？若存在，求出实数a的值．
  组卷：3引用：1难度：0.6

  解析