2022-2023学年河北省石家庄市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知复数z=

  3

  +

  2

  i

  3

  -

  2

  i

  ，则

  z

  在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：152引用：4难度：0.8

  解析

• 2．下列两项调查适宜采用的抽样方法依次是（　　）
  ①一项对“中兴事件”（2018年4月16日，美国对中兴通讯施行惩罚措施，引起国内关于国产芯片的讨论）影响的调查中有10000人认为这是美国贸易保护主义，对世界经济会产生比较负面的影响；有9000人认为这只是一个孤立事件，对世界经济大格局不会产生太大影响；有1000人没有发表自己的看法．现要从这20000人中随机抽取200人做进一步调查．
  ②从某中学高二年级的15名艺术特长生中选出3名调查学习负担情况．

  A．①简单随机抽样，②系统抽样

  B．①分层抽样，②简单随机抽样

  C．①系统抽样，②分层抽样

  D．①②都用分层抽样
  组卷：41引用：1难度：0.9

  解析

• 3．一个直三棱柱容器中盛有水，侧棱AA'=12．若侧面AA'B'B水平放置时，如图所示，水面恰好过AC、BC、A'C'、B'C'的中点，那么，当底面ABC水平放置时，水面高为（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：75引用：3难度：0.7

  解析

• 4．已知向量

  a

  =（1，m），

  b

  =（0，-2），且（

  a

  +

  b

  ）⊥

  b

  ，则m等于（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：86引用：4难度：0.7

  解析

• 5．已知a、b表示两条不同的直线，α，β表示两个不同的平面，则下列命题正确的是（　　）

  A．若α∥β，a∥α，b∥β，则a∥b	B．若a⊂α，b⊂β，a∥b,则α∥β
  C．若a⊥α，b⊥β，α⊥β，则a∥b	D．若a⊥α，b⊥β，a⊥b,则α⊥β
  组卷：168引用：3难度：0.9

  解析

• 6．△ABC的三边分别为a,b,c,且a=1，B=45°，S_△ABC=2，则△ABC的外接圆的直径为（　　）

  A．5

  B． 5 2

  C． 4 3

  D． 6 2
  组卷：993引用：15难度：0.9

  解析

• 7．已知

  sin

  （

  α

  +

  π

  3

  ）

  =

  1

  3

  ，则

  sin

  （

  2

  α

  +

  π

  6

  ）

  的值是（　　）

  A． 7 9

  B． - 7 9

  C． 2 9

  D． - 2 9
  组卷：479引用：8难度：0.6

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．

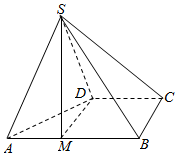• 21．四棱锥S-ABCD的底面ABCD为直角梯形，AB∥CD，AB⊥BC，AB=2BC=2CD=2，△SAD为正三角形．
  （Ⅰ）点M为棱AB上一点，若BC∥平面SDM，

  AM

  =

  λ

  AB

  ，求实数λ的值；
  （Ⅱ）若BC⊥SD，求点B到平面SAD的距离．
  组卷：200引用：6难度：0.5

  解析

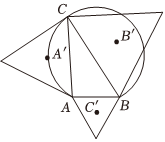• 22．拿破仑定理是法国著名军事家拿破仑最早提出的一个几何定理：“以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆圆心恰为另一个等边三角形（此等边三角形称为拿破仑三角形）的顶点．”某街角公园计划对园内的一块草坪进行改建，这块草坪是由一个半径为

  2

  6

  的圆的一段优弧与此圆弧上一条长为

  2

  6

  的弦AB围成，如图所示．改建计划是在优弧上选取一点C，以AC、BC、AB为边向外作三个等边三角形，其外心依次记为A'、B'、C'，在△A'B'C'区域内种植观赏花卉．
  （Ⅰ）设BC=a、AC=b,用a、b表示△A'B'C'的面积；
  （Ⅱ）要使△A'B'C'面积最大，C点应选在何处？并求出△A'B'C'面积最大值．
  组卷：35引用：1难度：0.4

  解析