2021-2022学年广东省广州八十六中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．若复数z=i（2+i）（i为虚数单位），则z的虚部为（　　）

  A．-1

  B．-2i

  C．2

  D．2i
  组卷：58引用：5难度：0.8

  解析

• 2．某田径队有男运动员56人，女运动员42人，若采用比例分配的分层随机抽样方法在这支田径队中抽取28人进行体质测试，则抽取男运动员的人数为（　　）

  A．16

  B．14

  C．12

  D．10
  组卷：49引用：2难度：0.9

  解析

• 3．某人在射击比赛中连续射击2次，事件“2次都不命中”的对立事件是（　　）

  A．至多有1次命中	B．2次都命中
  C．只有1次命中	D．至少有1次命中
  组卷：53引用：3难度：0.7

  解析

• 4．已知向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  b

  =

  （

  2

  ，

  λ

  ）

  （

  λ

  ∈

  R

  ）

  ，若

  a

  ⊥

  b

  ，则

  |

  a

  -

  b

  |

  =（　　）

  A．5

  B． 5 2

  C． 5 3

  D．10
  组卷：65引用：2难度：0.7

  解析

• 5．在3，5，7，11，13，17这6个数中随机选取两个不同的数，其和等于20的概率是（　　）

  A． 1 12

  B． 1 15

  C． 2 15

  D． 1 18
  组卷：39引用：2难度：0.8

  解析

• 6．参加某次数学竞赛的15名学生的成绩（单位：分）如下：
  75，71，73，86，88，76，80，81，96，84，50，99，83，92，91
  则这15人成绩的第80百分位数是（　　）

  A．90

  B．90.5

  C．91

  D．91.5
  组卷：58引用：1难度：0.9

  解析

• 7．若圆锥的底面半径为1，体积为

  3

  3

  π

  ，则该圆锥侧面展开图的面积是（　　）

  A．2π

  B．3π

  C．4π

  D．5π
  组卷：67引用：3难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

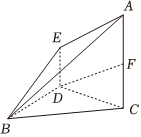• 21．如图，在四棱锥B-ACDE中，DE∥AC，AC⊥平面BCD，AC=2DE=4，BC=2，DC=1，∠BCD=60°，F为AC中点．
  （1）证明：DF∥平面ABE；
  （2）过点D作平行于平面ABE的截面，画出该截面，说明理由，并求夹在该截面与平面ABE之间的几何体的体积．
  组卷：70引用：2难度：0.5

  解析

• 22．某旅游景区内有一块等边三角形的景点ABC，其中AB=BC=AC=2（km）．
  
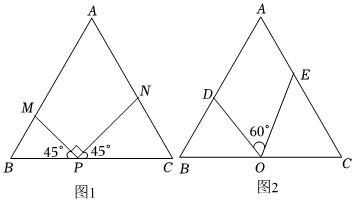
  （1）如图1，为迎接观光游，拟修建观赏小径PM，PN，其中M，N，P分别在AB，AC，BC上，且∠BPM=∠CPN=45°，问PM+PN是否为定值？说明理由；
  （2）如图2，为满足游客需求，拟修建两条商业街AD和AE，其中点D在AB上，点E在AC上．若O为BC中点，且∠DOE=60°，∠BOD=θ，求AD+AE的最大值及此时θ的值．
  组卷：30引用：2难度：0.5

  解析