2022-2023学年广东省东莞市七校联考高一(下)期中数学试卷
发布:2024/6/17 8:0:9
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
-
1.已知复数z=1-i,则z的虚部为( )
组卷:14引用:2难度:0.7 -
2.在△ABC中,已知
,a=3,B=45°,则A角的度数为( )b=2组卷:213引用:9难度:0.9 -
3.把一个铁制的底面半径为4,侧面积为
的实心圆柱熔化后铸成一个球,则这个铁球的半径为( )163π组卷:91引用:7难度:0.7 -
4.在△ABC中,D为BC的中点,E为AC边上的点,且
,则AE=3EC=( )ED组卷:485引用:12难度:0.8 -
5.α,β是两个不同的平面,m,n是两条不同的直线,则下列命题中正确的是( )
组卷:219引用:2难度:0.8 -
6.记△ABC的内角A,B,C的对边分别为a,b,c,a=2,c=3,
,则AC边上的高为( )B=π3组卷:82引用:4难度:0.7 -
7.在等腰三角形ABC中,AB=AC=
,BC=2,若P为边BC上的动点,则5•(AP+AB)=( )AC组卷:343引用:12难度:0.5
四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.解答应写出文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
-
21.记△ABC的内角A,B,C的对边分别为a,b,c,向量
,a=(cosB,sinB),且b=(2cosA-cosB,-2sinA-sinB).a⊥b
(1)求C;
(2)若c=6,求△ABC周长的取值范围.组卷:217引用:4难度:0.6 -
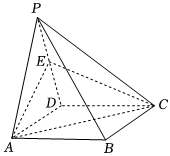 22.如图,四棱锥P-ABCD的底面是矩形,E为侧棱PD的中点,侧面PAD是正三角形,且侧面PAD⊥底面ABCD.
22.如图,四棱锥P-ABCD的底面是矩形,E为侧棱PD的中点,侧面PAD是正三角形,且侧面PAD⊥底面ABCD.
(1)求证:AE⊥平面PCD;
(2)当为何值时,使得PB⊥AC?请说明你的理由.ADAB组卷:118引用:1难度:0.6


