2022-2023学年福建省厦门市思明区大同中学九年级（上）期中数学试卷

一、选择题（本题共8小题，每小题4分，共32分.每小题只有一项是符合题目要求）

• 1．一元二次方程2x²-5x+1=0的一次项系数是（　　）

  A．-5

  B．0

  C．1

  D．2
  组卷：51引用：4难度：0.9

  解析

• 2．下列事件是随机事件的是（　　）

  A．任意一个三角形，它的内角和等于180°

  B．掷一枚硬币，正面朝上

  C．抛掷一枚各面点数分别是1至6点的骰子，出现点数是8

  D．明天太阳从西边升起
  组卷：74引用：3难度：0.8

  解析

• 3．数学世界中充满了许多美妙的几何图形，等待着你去发现，如图是张老师用几何画板画出的四个图形，其中既是轴对称图形又是中心对称图形的是（　　）
  

  A．①勾股树	B．②分形树
  C．③谢尔宾斯三角形	D．④雪花
  组卷：231引用：18难度：0.9

  解析

• 4．取3张扑克牌，其中1张“黑桃”，2张“梅花”，将这些扑克牌背面朝上从中任抽一张，恰好是“梅花”的概率是（　　）

  A． 1 2

  B． 1 3

  C． 2 3

  D． 2 5
  组卷：20引用：2难度：0.5

  解析

• 5．如图，已知点O是△ABC的外心，连结OB，OC，若∠BOC=80°，则∠A的度数是（　　）

  A．80°

  B．60°

  C．40°

  D．20°
  组卷：55引用：2难度：0.5

  解析

• 6．若x=2是关于x的一元二次方程3x²-mx-2=0的一个解．则m的值是（　　）

  A．6

  B．5

  C．2

  D．-6
  组卷：26引用：2难度：0.6

  解析

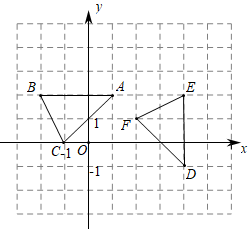• 7．如图，在平面直角坐标系中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，其中A、B、C分别和D、E、F对应，则旋转中心的坐标是（　　）

  A．（0，0）

  B．（1，0）

  C．（1，-1）

  D．（0.5，0.5）
  组卷：934引用：7难度：0.5

  解析

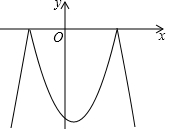• 8．已知二次函数y=-x²+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=-x+m与新图象有4个交点时，m的取值范围是（　　）

  A．- 25 4 ＜m＜3

  B．- 25 4 ＜m＜2

  C．-2＜m＜3

  D．-6＜m＜-2
  组卷：6415引用：25难度：0.7

  解析

三、解答题：本题共10小题，共86分，解答应写出文字说明、证明过程或演算步骤.

• 25．定义：有且仅有一组对角相等的凸四边形叫做“准平行四边形”，例如：凸四边形ABCD中，若∠A=∠C，∠B≠∠D，则称四边形ABCD为准平行四边形．
  （1）如图（1），A、P、B、C是⊙O上的四个点，∠APC=∠CPB=60°，延长BP到Q，使AQ=AP．已知∠QAC≠∠QBC，求证：四边形AQBC是准平行四边形；
  （2）如图（2），准平行四边形ABCD内接于⊙O，AB≠AD，BC=DC，若⊙O的半径为5，AB=6，求四边形ABCD的面积；
  （3）如图（3），在Rt△ABC中，∠C=90°，∠A=30°，BC=2，若四边形ABCD是准平行四边形，且∠BCD≠∠BAD，求BD长的最大值．
  
  组卷：736引用：8难度：0.2

  解析

• 26．如图，在平面直角坐标系中，抛物线y=x²+bx+c经过A（-1，0）、C（0，-3）两点，且与x轴交于另一点B（点B在点A右侧）．
  （1）求抛物线的解析式；
  （2）若点M是线段BC上一动点，过点M的直线ED平行y轴交x轴于点D，交抛物线于点E，求ME的最大值及此时点M的坐标；
  （3）在（2）的条件下：当ME取得最大值时，在x轴上是否存在这样的点P，使得以点M，B，P为顶点的三角形是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
  组卷：8引用：5难度：0.1

  解析