当前位置：试卷中心 > 试卷详情

2022-2023学年广西南宁二中高一（下）期末数学试卷

发布：2024/6/9 8:0:9

一、单选题（本大题共8小题，共40分．在每小题列出的选项中，选出符合题目的一项）．

1．已知a为实数，若复数z=（a²-1）+（a+1）i为纯虚数，则
a
+
i
2023
1
+
i
=（　　）
A．i B．-i C．1 D．-1
组卷：116引用：4难度：0.9
解析
2．我国古代数学名著《九章算术》有一抽样问题：“今有北乡若干人，西乡三百人，南乡两百人，凡三乡，发役六十人，而北乡需遗十，问北乡人数几何？“其意思为：“今有某地北面若干人，西面有300人，南面有200人，这三面要征调60人，而北面共征调10人（用分层抽样的方法），则北面共有（　　）人．”
A．200 B．100 C．400 D．300
组卷：12引用：2难度：0.8
解析
3．一个斜边长为2的等腰直角三角形绕斜边旋转一周，所形成的几何体的表面积为（　　）
A．4π B．
2
π
3
C．
2
π
D．
2
2
π
组卷：185引用：2难度：0.8
解析
4．设α，β是互不重合的平面，l,m,n是互不重合的直线，下列命题中正确的是（　　）
A．若m⊂α，n⊂β，m∥n,则α∥β
B．若α⊥β，α∩β=l,m⊥l,m⊂α，则m⊥β
C．若α∥β，m⊂α，n⊂β，则m∥n
D．若m⊥l,n⊥l,m⊂α，n⊂α，则l⊥α
组卷：170引用：5难度：0.7
解析
5．已知某人射击每次击中目标的概率都是0.6，现采用随机模拟的方法估计其3次射击至少2次击中目标的概率p.先由计算器产生0到9之间的整数值的随机数，指定0，1，2，3，4，5表示击中目标，6，7，8，9表示未击中目标；因为射击3次，所以每3个随机数为一组，代表3次射击的结果．经随机模拟产生了以下20组随机数：
169 966 151 525 271 937 592 408 569 683
471 257 333 027 554 488 730 863 537 039
据此估计p的值为（　　）
A．0.6 B．0.65 C．0.7 D．0.75
组卷：249引用：7难度：0.8
解析
6．设a=sin14°+cos14°，b=sin16°+cos16°，
c
=
6
2
，则下列结论正确的是（　　）
A．a＜b＜c B．b＜a＜c C．c＜b＜a D．a＜c＜b
组卷：46引用：1难度：0.7
解析
7．已知正四面体ABCD，M为BC中点，N为AD中点，则直线BN与直线DM所成角的余弦值为（　　）
A．
1
6
B．
2
3
C．
21
21
D．
4
21
21
组卷：180引用：10难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分，其中17题10分，其余小题每题12分．解答应写出文字说明，证明过程或演算步骤）

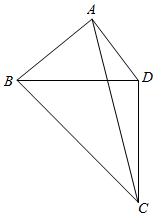21．为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形ABCD．其中AB=3百米，AD=
5
百米，且△BCD是以D为直角顶点的等腰直角三角形．拟修建两条小路AC，BD（路的宽度忽略不计），设∠BAD=θ，θ∈（
π
2
，π）．
（1）当cosθ=
-
5
5
时，求小路AC的长度；
（2）当草坪ABCD的面积最大时，求此时小路BD的长度．
组卷：748引用：19难度：0.4
解析
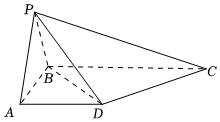22．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AD⊥AB，平面PAB⊥平面PBC，
AD
=
1
2
BC
=
6
，
AB
=
AP
=
3
．
（1）求证：AD⊥PB；
（2）若PD与平面PBC所成的角为30°，求二面角B-PD-C的余弦值．
组卷：292引用：2难度：0.5
解析