2023-2024学年山东省部分学校（中）高三（上）月考数学试卷（10月份）

一、单项选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题要求的。

• 1．下列各式中，值为

  -

  3

  4

  的是（　　）

  A．2sin15°•cos15°	B．cos215°-sin215°
  C．2sin215°-1	D． 1 2 - co s 2 15 °
  组卷：33引用：4难度：0.9

  解析

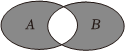• 2．如图所示的韦恩图中，A，B是非空集合，定义集合A#B为阴影部分表示的集合．若x,y∈R，A={x|y=

  2

  x

  -

  x

  2

  }，B={y|y=3^x，x＞0}，则A#B=（　　）

  A．{x|0＜x＜2}	B．{x|1＜x≤2}
  C．{x|0≤x≤1或x≥2}	D．{x|0≤x≤1或x＞2}
  组卷：130引用：19难度：0.9

  解析

• 3．将函数f（x）=2sin

  （

  ωx

  -

  π

  3

  ）

  （

  ω

  ＞

  0

  ）

  的图象向左平移

  π

  3

  ω

  个单位，得到函数y=g（x）的图象．若y=g（x）在[

  0

  ，

  π

  4

  ]上为增函数，则ω的最大值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：60引用：12难度：0.9

  解析

• 4．化简（

  a

  2

  3

  b

  1

  2

  ）×（-

  3

  a

  1

  2

  b

  1

  3

  ）÷（

  1

  3

  a

  1

  6

  b

  5

  6

  ）的结果（　　）

  A．6a

  B．-a

  C．-9a

  D．9a2
  组卷：336引用：30难度：0.9

  解析

• 5．已知3^a=5^b=A，且

  1

  a

  +

  1

  b

  =2，则A的值是（　　）

  A．15

  B． 15

  C．± 15

  D．225
  组卷：434引用：24难度：0.9

  解析

• 6．给出下列命题①∀x∈R，x²+1＞0；②∀x∈N，x⁴≥1；③∃x∈Z，x³＜1；④∀x∈Q，x²≠2．其中真命题有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：7引用：3难度：0.8

  解析

• 7．若f（x）=-x²+ax+2+lg（2-|x|）（a∈R）是偶函数，且f（1-m）＜f（m），则实数m的取值范围是（　　）

  A．（ 1 2 ，+∞）

  B．（-∞， 1 2 ）

  C．（ 1 2 ，2）

  D．（-1， 1 2 ）
  组卷：32引用：3难度：0.7

  解析

四、解答题：（本大题共6个小题，满分70分，解答应写出必要的文字说明、证明过程和演算步骤。）

• 21．已知函数f（x）=alnx-2ax+3（a≠0）．
  （1）求函数f（x）的极值；
  （2）若函数y=f（x）的图象在x=2处的切线的斜率为

  3

  2

  ，

  g

  （

  x

  ）

  =

  1

  3

  x

  3

  +

  x

  2

  [

  f

  ′

  （

  x

  ）

  +

  m

  ]

  在区间（1，3）上不是单调函数，且当x∈（0，1]时f（x）不小于

  2

  3

  x

  3

  -

  2

  m

  ，求实数m的取值范围．
  组卷：17引用：2难度：0.6

  解析

• 22．已知函数f（x）=lnx,g（x）=e^x（e^x=2.718…，e为自然对数的底数）
  （1）求函数F（x）=f（x）-g（x-1）的单调区间；
  （2）若不等式xf（x）-k（x+1）f[g（x-1）]≤0在区间[1，+∞）上恒成立，求实数k的取值范围．
  组卷：18引用：6难度：0.5

  解析