2023-2024学年湖北省武汉四十九中高三（上）月考数学试卷（9月份）（二）

一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合A={x|x²-2x-3＜0}，B={y|y=e^x}，则A∩B=（　　）

  A．∅

  B．（-1，+∞）

  C．（0，3）

  D．（1，3）
  组卷：55引用：7难度：0.7

  解析

• 2．已知复数z=

  2

  i

  1

  -

  i

  ，则下列结论正确的是（　　）

  A．z在复平面对应的点位于第三象限

  B．z的虚部是i

  C．|z|= 2

  D． z =1+i
  组卷：185引用：7难度：0.7

  解析

• 3．已知△ABC的外接圆圆心为O，且

  AO

  =

  AB

  +

  AC

  ，则

  BA

  在

  BC

  上的投影向量为（　　）

  A． 1 2 BC

  B． - 1 2 BC

  C． 1 4 BC

  D． - 1 4 BC
  组卷：32引用：3难度：0.8

  解析

• 4．已知函数

  f

  （

  x

  ）

  =

  x 2 + ax + 1 ， x ≥ 1

  a x 2 + x + 1 ， x ＜ 1

  则“-2≤a≤0”是“f（x）在R上单调递增”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：122引用：7难度：0.7

  解析

• 5．若直线l：kx-y-2=0与曲线

  C

  ：

  1

  -

  （

  y

  -

  1

  ）

  2

  =

  x

  -

  1

  有两个交点，则实数k的取值范围是（　　）

  A． （ 4 3 ， 2 ]	B． （ 4 3 ， 4 ）
  C． [ - 2 ， 4 3 ） ∪ （ 4 3 ， 2 ]	D． （ 4 3 ， + ∞ ）
  组卷：486引用：36难度：0.6

  解析

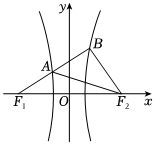• 6．如图所示，点F₁，F₂是双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦点，双曲线C的右支上存在一点B满足BF₁⊥BF₂，BF₁与双曲线C的左支的交点A平分线段BF₁，则双曲线C的渐近线斜率为（　　）

  A．±3

  B． ± 2 3

  C． ± 13

  D． ± 15
  组卷：278引用：5难度：0.6

  解析

• 7．已知S_n是等比数列{a_n}的前n项和，且

  S

  n

  =

  2

  n

  +

  1

  +

  a

  ，则a₁a₂+a₂a₃+⋯+a₁₀a₁₁=（　　）

  A． 2 23 - 8 3

  B． 2 13 - 8 3

  C． 2 20 - 1 3

  D． 2 25 - 8 3
  组卷：372引用：6难度：0.6

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.

• 21．甲、乙两人进行象棋比赛，赛前每人发3枚筹码．一局后负的一方，需将自己的一枚筹码给对方；若平局，双方的筹码不动，当一方无筹码时，比赛结束，另一方最终获胜．由以往两人的比赛结果可知，在一局中甲胜的概率为0.3、乙胜的概率为0.2．
  （1）第一局比赛后，甲的筹码个数记为X，求X的分布列和期望；
  （2）求四局比赛后，比赛结束的概率；
  （3）若P_i（i=0，1，⋯，6）表示“在甲所得筹码为i枚时，最终甲获胜的概率”，则P₀=0，P₆=1．证明：{P_i+1-P_i}（i=0，1，2，⋯，5）为等比数列．
  组卷：269引用：5难度：0.4

  解析

• 22．已知定点F（1，0），定直线l：x=-1，动圆M过点F，且与直线l相切．
  （1）求动圆的圆心M所在轨迹C的方程；
  （2）已知点P（t,-1）是轨迹C上一点，点A，B是轨迹C上不同的两点（点A，B均不与点P重合），设直线AP，BP的斜率分别为k₁、k₂，且满足

  k

  1

  +

  k

  2

  =

  -

  8

  5

  ，证明：直线AB过定点，并求出定点的坐标．
  组卷：82引用：6难度：0.5

  解析