当前位置：试卷中心 > 试卷详情

2022-2023学年吉林省长春第108学校九年级（上）月考数学试卷

发布：2024/9/11 9:0:9

一、选择题（每题3分，共24分）

1．方程x²-2x=0的根是（　　）
A．x₁=x₂=0 B．x₁=x₂=2 C．x₁=0，x₂=2 D．x₁=0，x₂=-2
组卷：257引用：12难度：0.7
解析
2．抛物线y=-（x-4）²-3的顶点坐标是（　　）
A．（-4，3） B．（-4，-3） C．（4，3） D．（4，-3）
组卷：292引用：4难度：0.9
解析
3．如图所示，A（2
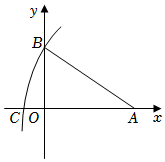2
，0），AB=3
2
，以点A为圆心，AB长为半径画弧交x轴负半轴于点C，则点C的坐标为（　　）
A．（3
2
，0） B．（
2
，0） C．（-
2
，0） D．（-3
2
，0）
组卷：1548引用：15难度：0.9
解析
4．若二次函数y=ax²的图象经过点P（-2，4），则该图象必经过点（　　）
A．（2，4） B．（-2，-4） C．（-4，2） D．（4，-2）
组卷：4276引用：169难度：0.9
解析
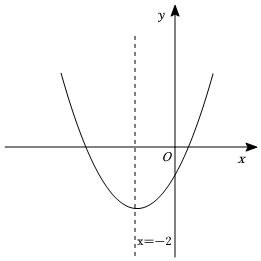5．如图，抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=-2，下列结论正确的是（　　）
A．a＜0
B．c＞0
C．当x＜-2时，y随x的增大而减小
D．当x＞-2时，y随x的增大而减小
组卷：3307引用：16难度：0.6
解析
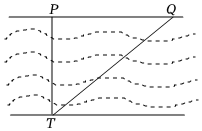6．如图，一条河的两岸互相平行，为了测量河的宽度PT（PT与河岸PQ垂直），测量得P，Q两点间距离为m米，∠PQT=α，则河宽PT的长为（　　）
A．msinα B．mcosα C．mtanα D．
m
tanα
组卷：1947引用：19难度：0.6
解析
7．在平面直角坐标系中，将抛物线y=x²+2x-1，绕原点旋转180°，所得到的抛物线的函数关系式是（　　）
A．y=x²-2x+1 B．y=-x²-2x-1 C．y=-x²+2x-1 D．y=-x²+2x+1
组卷：32引用：1难度：0.5
解析
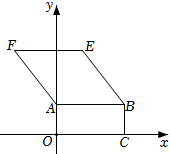8．如图，在平面直角坐标系xOy中，矩形OABC的顶点B的坐标为（10，4），四边形ABEF是菱形，且tan∠ABE=
4
3
．若直线l把矩形OABC和菱形ABEF的面积都分成相等的两部分，则直线l的解析式为（　　）
A．y=3x B．y=-
3
4
x+
15
2
C．y=-2x+11 D．y=-2x+12
组卷：1895引用：5难度：0.4
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，共78分＞

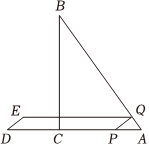23．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8．动点P以每秒5个单位长度的速度从点A出发，沿A→C→B的方向向终点B运动．点P关于点C的对称点为D，当点P不与A、B重合时，过点P作PQ⊥AB于点Q，以PD，PQ为边作平行四边形PDEQ．设点P的运动时间为t（s）．
（1）用含t的代数式表示PQ的长．
（2）当平行四边形PDEQ为菱形时，求t的值．
（3）当△ABC的某条直角边将平行四边形PDEQ的面积分成3：5两部分时，求t的值．
（4）作点E关于直线PQ的对称点F，当点F落在△ABC内部时，直接写出t的取值范围．
组卷：27引用：2难度：0.3
解析
24．如图，在平面直角坐标系中，抛物线C₁：y=x²+bx+c经过点A（1，0），点B（0，5），点P在该抛物线上，其横坐标为m.
（1）求抛物线C₁的解析式，并在网格中画出抛物线C₁的函数图象．
（2）当点P到抛物线C₁对称轴的距离小于2时，直接写出点P的纵坐标的取值范围．
（3）当m=3时，把抛物线C₁沿y轴向上平移得到抛物线C₂，平移的距离为h（h＞0），在平移过程中，抛物线C₂与直线BP始终有交点，求h的最大值．
（4）若抛物线C₁在点P左侧部分（包括点P）的最低点的纵坐标为3-m,求m的值．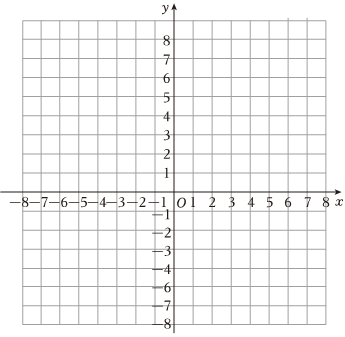
组卷：25引用：1难度：0.1
解析