2022-2023学年江苏省扬州大学附中高一（上）月考数学试卷（12月份）

一、单选题

• 1．已知全集U={1，2，3，4，5}，A={2，3}，B={1，3}，则∁_U（A∩B）=（　　）

  A．{3}

  B．{4，5}

  C．{1，2，4，5}

  D．{1，2，3，5}
  组卷：96引用：3难度：0.9

  解析

• 2．命题“∀x≥1，x²≥1“的否定是（　　）

  A．∃x≥1，x2＜1

  B．∃x＜1，x2≥1

  C．∃x≥1，x2≥1

  D．∃x＜1，x2＜1
  组卷：11引用：5难度：0.9

  解析

• 3．若幂函数y=f（x）的图象过点（4，2），则f（2）的值为（　　）

  A．2

  B． 1 2

  C． 2

  D．4
  组卷：250引用：5难度：0.9

  解析

• 4．已知函数y=a^x+4+2（a＞0，且a≠1）的图象恒过点P，若角α的终边经过点P，则cosα的值为（　　）

  A． - 4 5

  B． - 2 2 3

  C． 2 3

  D． 3 5
  组卷：210引用：3难度：0.7

  解析

• 5．a=sin1，b=lgsin1，c=10^sin1，则（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜b＜a
  组卷：100引用：7难度：0.7

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  cos

  4

  x

  2

  x

  -

  2

  -

  x

  ，则f（x）的图像大致是（　　）

  A．

  B．

  C．

  D．
  组卷：81引用：2难度：0.7

  解析

• 7．设m,n为正数，且m+n=2，则

  4

  m

  +

  1

  +

  1

  n

  +

  1

  的最小值为（　　）

  A． 13 4

  B． 9 4

  C． 7 4

  D． 9 5
  组卷：611引用：4难度：0.6

  解析

四、解答题

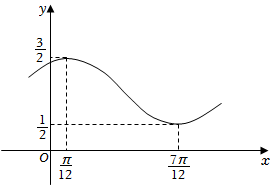• 21．已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜

  π

  2

  ）的部分图象如图所示．
  （1）求函数f（x）的解析式；
  （2）将函数y=f（x）的图象上所有的点向右平移

  π

  12

  个单位，再将所得图象上每一个点的横坐标变为原来的2倍（纵坐标不变），得到函数y=g（x）的图象．
  ①当x∈[-

  π

  3

  ，

  π

  2

  ]时，求函数g（x）的值域；
  ②若方程g（x）-m=0在[0，

  7

  π

  3

  ]上有三个不相等的实数根x₁，x₂，x₃（x₁＜x₂＜x₃），求tan（x₁+2x₂+x₃）的值．
  组卷：529引用：7难度：0.5

  解析

• 22．对于函数f（x），若在其定义域内存在实数x₀，t,使得f（x₀+t）=f（x₀）+f（t）成立，则称f（x）是“t跃点”函数，并称x₀是函数f（x）的1个“t跃点”．
  （1）求证：函数f（x）=2^x+2x²在[0，1]上是“1跃点”函数；
  （2）是否同时存在实数m和正整数n使得函数h（x）=cos2x-m在[0，nπ]上有2022个“

  π

  2

  跃点”？若存在，请求出m和n满足的条件；若不存在，请说明理由．
  组卷：7引用：1难度：0.5

  解析