2023-2024学年甘肃省武威市民勤一中高一（上）分班数学试卷

一、单项选择题（本题共10小题，每小题4分，共40分．1-8是单选，9-10是多选）

• 1．二次根式

  1

  -

  2

  x

  有意义，则x应满足的条件是（　　）

  A． x = 1 2

  B． x ≤ 1 2

  C． x ＜ 1 2

  D． x ≥ 1 2
  组卷：56引用：1难度：0.8

  解析

• 2．已知p²+q²=169，p-q=7，那么pq的值为（　　）

  A．120

  B．60

  C．30

  D．15
  组卷：109引用：1难度：0.9

  解析

• 3．多项式x²-3x+a可分解为（x-5）（x-b），则a,b的值分别为（　　）

  A．10，-2

  B．-10，2

  C．10，2

  D．-10，-2
  组卷：16引用：1难度：0.8

  解析

• 4．已知集合A={x|1≤x≤3}，B={x|2＜x＜4}，U=R，则A∩（∁_UB）=（　　）

  A．{x|2＜x≤3}

  B．{x|1≤x≤2}

  C．{x|x≤3或x≥4}

  D．{x|2≤x＜4}
  组卷：58引用：4难度：0.8

  解析

• 5．若a,b,c是△ABC的三条边，且a³-b³=a²b-ab²+ac²-bc²，则这个三角形是（　　）

  A．等腰三角形

  B．直角三角形

  C．等腰直角三角形

  D．等腰三角形或直角三角形
  组卷：93引用：1难度：0.8

  解析

• 6．已知关于x的方程x²-4x+c=0的两根分别是x₁，x₂，且满足

  x

  1

  x

  2

  +

  x

  2

  x

  1

  =

  6

  ，则实数c的值为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：123引用：5难度：0.7

  解析

三、解答题（本题共4小题，共44分）

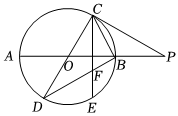• 17．如图，AB，CD为圆的直径，C为圆O上一点，过点C的切线与AB的延长线交于点P，∠ABC=2∠BCP，点E是弧BD的中点，弦CE，BD相交于点F．
  （1）求∠OCB的度数；
  （2）若EF=3，求圆O直径的长．
  组卷：20引用：3难度：0.6

  解析

• 18．如图，抛物线

  y

  =

  -

  3

  x

  2

  +

  bx

  +

  c

  交x轴于点A（-1，0）和B，交y轴于点

  C

  （

  0

  ，

  3

  3

  ）

  ，顶点为D．
  （1）求抛物线的表达式；
  （2）若点E在第一象限内对称轴右侧的抛物线上，四边形ODEB的面积为

  7

  3

  ，求点E的坐标；
  （3）在（2）的条件下，若点F是对称轴上一点，点H是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G，使以E，F，G，H为顶点的四边形是菱形，且∠EFG=60°，如果存在，请直接写出点G的坐标；如果不存在，请说明理由．
  组卷：19引用：3难度：0.5

  解析