2023-2024学年福建省厦门一中高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若直线l₁：x-y=0与直线l₂：x+ay+2=0互相垂直，则a的值为（　　）

  A．-1

  B．1

  C．-2

  D．2
  组卷：68引用：4难度：0.8

  解析

• 2．已知向量

  a

  =（2x,1，3），

  b

  =（1，-2y,9），若

  a

  ∥

  b

  ，则（　　）

  A．x=1，y=1

  B．x= 1 2 ，y=- 1 2

  C．x= 1 6 ，y=- 3 2

  D．x=- 1 6 ，y= 3 2
  组卷：383引用：40难度：0.9

  解析

• 3．“m＞2”“是方程

  x

  2

  m

  2

  +

  y

  2

  m

  +

  2

  =

  1

  表示焦点在x轴上的椭圆”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：549引用：6难度：0.7

  解析

• 4．中心在原点，焦点在x轴上的双曲线的一条渐近线经过点（4，-2），则它的离心率为（　　）

  A． 6

  B． 5

  C． 6 2

  D． 5 2
  组卷：205引用：16难度：0.9

  解析

• 5．F₁为双曲线C：

  x

  2

  9

  -

  y

  2

  16

  =

  1

  的左焦点，双曲线C的右支上的三个不同的点P₁，P₂，P₃关于y轴的对称点分别为P₄，P₅，P₆，则|P₁F₁|+|P₂F₁|+|P₃F₁|-|P₄F₁|-|P₅F₁|-|P₆F₁|的值为（　　）

  A．12

  B．16

  C．18

  D．24
  组卷：72引用：1难度：0.7

  解析

• 6．在正方体ABCD-A₁B₁C₁D₁中，点O为线段BD的中点．设点P在线段BB₁（P不与B重合）上，直线OP与平面A₁BD所成的角为α，则sinα的最大值是（　　）

  A． 1 3

  B． 2 3

  C． 3 3

  D． 3 4
  组卷：87引用：2难度：0.5

  解析

• 7．数学美的表现形式不同于自然美或艺术美那样直观，它蕴藏于特有的抽象概念，公式符号，推理论证，思维方法等之中，揭示了规律性，是一种科学的真实美．平面直角坐标系中，曲线C：x²+y²=|x|+|y|就是一条形状优美的曲线，若P（m,n）是曲线C上任意一点，则|m+n-3|的最小值是（　　）

  A． 2 2

  B．1

  C． 2

  D．2
  组卷：86引用：2难度：0.5

  解析

四、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.

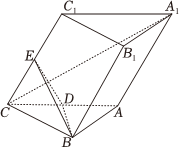• 21．如图，在三棱柱ABC-A₁B₁C₁中，底面是边长为2的等边三角形，CC₁=2，D，E分别是线段AC，CC₁的中点，C₁在平面ABC内的射影为D．
  （1）求证：A₁C⊥平面BDE；
  （2）若点F为棱B₁C₁的中点，求点F到平面BDE的距离；
  （3）若点F为线段B₁C₁上的动点（不包括端点），求平面FBD与平面BDE夹角的余弦值的取值范围．
  ​
  组卷：130引用：10难度：0.6

  解析

• 22．已知点A（2，1）在椭圆C：

  x

  2

  a

  2

  +

  y

  2

  a

  2

  -

  3

  =1上，直线l交C于点P，Q，直线AP，AQ的斜率之和为0．
  （1）求l的斜率；
  （2）若tan∠PAQ=

  4

  3

  ，求△PAQ的面积．
  组卷：70引用：2难度：0.3

  解析