2022-2023学年江苏省常州市教育学会高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知z为复数，

  z

  为z的共轭复数，且

  z

  =

  |

  z

  |

  -

  1

  +

  5

  i

  ，则z的虚部是（　　）

  A．5i

  B．-5i

  C．5

  D．-5
  组卷：43引用：1难度：0.8

  解析

• 2．设a,b是两条不同的直线，α，β是两个不同的平面，则能得出a⊥b的是（　　）

  A．a⊥α，b∥β，α⊥β	B．a⊥α，b⊥β，α∥β
  C．a⊂α，b⊥β，α∥β	D．a⊂α，b∥β，α⊥β
  组卷：970引用：31难度：0.9

  解析

• 3．投掷3枚质地均匀的正方体骰子，观察正面向上的点数，则对于这3个点数，下列说法正确的是（　　）

  A．有且只有1个奇数的概率为 1 8

  B．事件“都是奇数”和事件“都是偶数”是对立事件

  C．在已知有奇数的条件下，至少有2个奇数的概率为 4 7

  D．事件“至少有1个是奇数”和事件“至少有1个是偶数”是互斥事件
  组卷：75引用：2难度：0.7

  解析

• 4．已知平面上的三点A，B，C满足|AB|=2，

  |

  BC

  |

  =

  2

  ，向量

  AB

  与

  BC

  的夹角为45°，且

  （

  λ

  BC

  -

  AB

  ）

  ⊥

  AB

  ，则实数λ=（　　）

  A．0

  B．1

  C．-2

  D．2
  组卷：46引用：1难度：0.8

  解析

• 5．一个不透明的盒子里装有10个大小形状都相同的小球，其中3个黑色、7个白色，现在3个人依次从中随机地各取一个小球，前一个人取出一个小球记录颜色后放回盒子，后一个人接着取球，则这3个人中恰有一人取到黑球的概率为（　　）

  A． 3 10	B． 3 A 2 7 • A 1 3 A 3 10
  C． C 3 10 × 0 . 7 2 × 0 . 3	D． C 1 3 × 0 . 7 2 × 0 . 3
  组卷：47引用：1难度：0.7

  解析

• 6．已知圆锥的高为1，体积为π，则过圆锥顶点作圆锥截面的面积最大值为（　　）

  A． 3

  B．2

  C． 2 3 π

  D．3π
  组卷：103引用：3难度：0.5

  解析

• 7．对一个十位数1234567890，现将其中3个数位上的数字进行调换，使得这3个数字都不在原来的数位上，其他数位上的数字不变，则可以得到不同的十位数（首位不为0）的个数为（　　）

  A．120

  B．232

  C．240

  D．360
  组卷：80引用：1难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．记f_n（x）=（x+1）ⁿ=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n，n∈N^*．
  （1）化简：

  n

  ∑

  i

  =

  1

  （

  i

  +

  1

  ）

  a

  i

  ；
  （2）证明：f_n+1（x）+2f_n+2（x）+…+kf_n+k（x）+…+nf_2n（x）（n∈N^*）的展开式中含xⁿ项的系数为（n+1）

  C

  n

  +

  2

  2

  n

  +

  1

  ．
  组卷：62引用：1难度：0.5

  解析

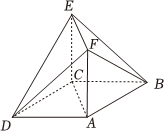• 22．如图，在多面体EF-ABCD中，底面ABCD是菱形，且CE⊥底面ABCD，AF∥CE，AC=CD=CE=AF=1，点M在线段EF上．
  （1）若M为EF的中点，求直线AM和平面BDE的距离；
  （2）试确定M点位置，使二面角D-AM-B的余弦值为-

  35

  67

  ．
  组卷：77引用：1难度：0.6

  解析