2022-2023学年湖南省邵阳市高一（下）期末数学试卷

一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．实数m＞1时，复数m（3+i）-（2+i）在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：20引用：2难度：0.7

  解析

• 2．下列各组向量中，可以作为基底的是（　　）

  A． e 1 = （ 0 ， 0 ） ， e 2 = （ - 1 ， 3 ）	B． e 1 = （ 3 ，- 2 ） ， e 2 = （ - 6 ， 4 ）
  C． e 1 = （ 1 ， 2 ） ， e 2 = （ 2 ， 3 ）	D． e 1 = （ 1 ， 1 ） ， e 2 = （ 2 ， 2 ）
  组卷：115引用：9难度：0.8

  解析

• 3．某芯片制造厂有甲、乙、丙三条生产线均生产8nm规格的芯片．现有25块该规格的芯片，其中来自甲、乙、丙的芯片数量分别为5块、10块、10块．若甲、乙、丙生产的芯片的优质品率分别为0.8，0.8，0.7，则从这25块芯片中随机抽取一块，该芯片为优质品的概率是（　　）

  A．0.78

  B．0.76

  C．0.64

  D．0.58
  组卷：23引用：3难度：0.7

  解析

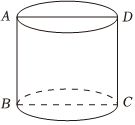• 4．如图，某圆柱体的高为1，ABCD是该圆柱体的轴截面．已知从点B出发沿着圆柱体的侧面到点D的路径中，最短路径的长度为

  5

  2

  ，则该圆柱体的侧面积是（　　）

  A．14

  B． 7 π

  C．7

  D． 32 π
  组卷：62引用：2难度：0.7

  解析

• 5．已知α，β表示两个不同的平面，m为平面α内的一条直线，则“m⊥β”是“α⊥β”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：308引用：10难度：0.9

  解析

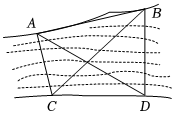• 6．如图，为测量河对岸A，B两点间的距离，沿河岸选取相距

  20

  3

  m

  的C，D两点，测得∠ACB=90°，∠BCD=30°，∠ADB=60°，∠ADC=30°，A，B两点的距离为（　　）

  A． 20 3 m

  B． 20 5 m

  C． 20 6 m

  D． 20 7 m
  组卷：36引用：2难度：0.6

  解析

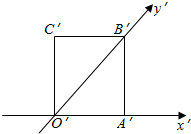• 7．如图所示，正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图，则原图形的面积是（　　）

  A．1cm2

  B．2 2 cm2

  C．3 2 cm2

  D． 2 4 cm2
  组卷：481引用：11难度：0.7

  解析

四、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）

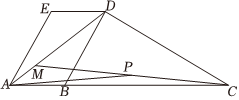• 21．如图，已知四边形ABDE为平行四边形，点C在AB延长线上，点M在线段AD上，且

  AB

  =

  1

  2

  BC

  ，

  AM

  =

  1

  3

  AD

  ，设

  AB

  =

  a

  ，

  AE

  =

  b

  ．
  （1）用向量

  a

  ，

  b

  表示

  CD

  ；
  （2）若线段CM上存在一动点P，且

  AP

  =

  m

  a

  +

  n

  b

  （

  m

  ,

  n

  ∈

  R

  ）

  ，求n²+mn的最大值．
  组卷：63引用：2难度：0.5

  解析

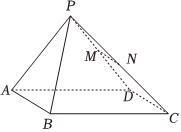• 22．如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面PAD⊥底面ABCD，M是线段PD的中点，N是线段PC的中点．
  （1）求证：MN∥平面PAB；
  （2）求PC与底面ABCD所成角的正切值．
  组卷：75引用：2难度：0.5

  解析