2022-2023学年安徽省六安一中高三（上）第四次月考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知复数z满足

  1

  +

  3

  i

  z

  =

  1

  -

  i

  （i为虚数单位），

  z

  是z的共轭复数，则复数

  z

  在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：32引用：3难度：0.8

  解析

• 2．已知空间中的两个不同的平面α，β，直线m⊥平面β，则“α⊥β”是“m∥α”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分又不必要条件
  组卷：128引用：12难度：0.7

  解析

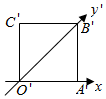• 3．一个水平放置的平面图形，用斜二测画法画出了它的直观图，如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形的面积为（　　）

  A． 2

  B． 4 2

  C．8

  D． 8 2
  组卷：447引用：5难度：0.8

  解析

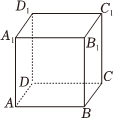• 4．如图，已知ABCD-A₁B₁C₁D₁是正方体，以下结论错误的是（　　）

  A．向量 AC 与向量 C 1 D 的夹角为60°

  B． A C 1 • A 1 B = 0

  C． （ A 1 A + A 1 D 1 + A 1 B 1 ） 2 = 3 A 1 B 1 2

  D．若 A 1 P = 1 3 A 1 C ，则点P是△AB1D1的中心
  组卷：4引用：2难度：0.7

  解析

• 5．若不等式

  16

  -

  x

  2

  ≤

  kx

  （

  k

  ＞

  0

  ）

  的解集为区间[a,b]，且b-a=2，则k=（　　）

  A． 3 3

  B． 2

  C． 3

  D．2
  组卷：10引用：2难度：0.8

  解析

• 6．过点P（-3，4）作圆C：x²+y²=25的切线l,直线m：ax-4y=0与切线l平行，则切线l与直线m间的距离为（　　）

  A．5

  B．2

  C．4

  D．3
  组卷：7引用：2难度：0.5

  解析

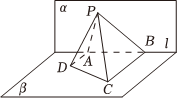• 7．如图，已知平面α⊥β，α∩β=l,A，B是直线l上的两点，C、D是平面β内的两点，且DA⊥l.CB⊥l,AD=3，AB=6，CB=6，P是平面α上的一动点，且直线PD、PC与平面α所成角相等，则四棱锥P-ABCD体积的最大值为（　　）

  A．18

  B．36

  C．24

  D．48
  组卷：6引用：2难度：0.6

  解析

四、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．

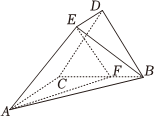• 21．在①AE=2，②AC⊥BD，③∠EAB=∠EBA，这三个条件中选择一个，补充在下面问题中，并给出解答．如图，在五面体ABCDE中，已知，AC⊥BC，ED∥AC，且

  AC

  =

  BC

  =

  2

  ED

  =

  2

  ，

  DC

  =

  DB

  =

  3

  ．
  （1）设平面BDE与平面ABC的交线为l,证明：l∥平面ACDE；
  （2）求证：平面ABE⊥平面ABC；
  （3）线段BC上是否存在一点F，使得平面AEF与平面ABF夹角的余弦值等于

  5

  43

  43

  ，若存在，求

  BF

  BC

  的值；若不存在，请说明理由．
  组卷：19引用：2难度：0.5

  解析

• 22．已知a,b∈R，函数f（x）=e^x-asinx,g（x）=b

  x

  ．
  （Ⅰ）求函数y=f（x）在点（0，f（0））处的切线方程；
  （Ⅱ）若曲线y=f（x）和y=g（x）有公共点，
  （ⅰ）当a=0时，求b的取值范围；
  （ⅱ）求证：a²+b²＞e.
  组卷：999引用：5难度：0.4

  解析