2022-2023学年安徽省阜阳市太和县三堂中学九年级（上）期中数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）

• 1．一元二次方程2x²-6x-5=0的一次项系数是（　　）

  A．2

  B．6

  C．-6

  D．-5
  组卷：45引用：7难度：0.7

  解析

• 2．下列是部分星座的符号，其中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：43引用：7难度：0.8

  解析

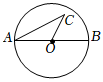• 3．如图，AB是⊙O的直径，C为圆内一点，则下列说法正确的是（　　）

  A．∠BOC是圆心角	B．AC是⊙O的弦
  C．∠C是圆周角	D． AC + OC ＜ 1 2 AB
  组卷：122引用：8难度：0.8

  解析

• 4．某种商品每天的销售利润y（元）与单价x（元）之间的函数关系式为y=-0.1（x-3）²+25．则这种商品每天的最大利润为（　　）

  A．0.1元

  B．3元

  C．25元

  D．75元
  组卷：282引用：7难度：0.9

  解析

• 5．某厂1月份生产口罩60万箱，第一季度生产口罩共200万箱，一位同学根据题意列出了方程60+60（1+x）+60（1+x）²=200，则x表示的意义是（　　）

  A．该厂二月份的增长率

  B．该厂三月份的增长率

  C．该厂一、二月份平均每月的增长率

  D．该厂二、三月份平均每月的增长率
  组卷：151引用：7难度：0.8

  解析

• 6．将抛物线y=2x²+3向右平移3个单位长度．再向上平移2个单位长度，得到的抛物线的解析式为（　　）

  A．y=2（x-3） 2+5	B．y=2（x-3） 2-1
  C．y=2（x+3） 2+5	D．y=2（x+3） 2-1
  组卷：108引用：8难度：0.8

  解析

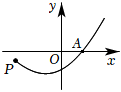• 7．如图，点P从右向左运动的运动路线在抛物线y=a（x+1）²-1上，点P第一次到达x轴时的坐标为A（1，0），则当点P再次到达x轴时的坐标为（　　）

  A．（-2，0）

  B．（-2.5，0）

  C．（-3，0）

  D．（-3.5，0）
  组卷：43引用：5难度：0.6

  解析

七、（本题满分12分）

• 22．已知抛物线y=x²+（2m+2）x+m²+m-1（m是常数）．
  （1）用含m的代数式表示该二次函数图象的顶点坐标．
  （2）当二次函数图象的顶点在x轴上时，求m的值及此时顶点的坐标．
  （3）小明研究发现：无论m取何值，抛物线的顶点都在同一条直线上．请写出这条直线的解析式，并加以证明．
  组卷：179引用：6难度：0.6

  解析

八、（本题满分14分）

• 23．综合与实践：
  已知△ABC与△BDE均为等腰直角三角形，其中∠BAC=∠BDE=90°，连接CE，P是EC的中点，连接PA，PD．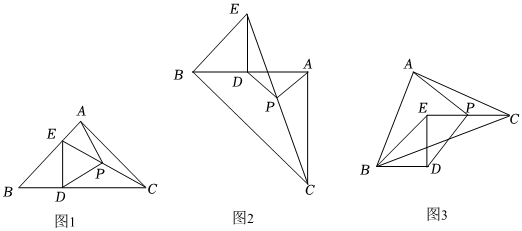
  
  【初步感知】（1）如图1，当B，D，C三点在同一直线上时，PA和PD的数量关系为

  ，位置关系为

  ．
  【深入探究】（2）如图2，当B，D，A三点在同一直线上时，（1）中得到的结论成立吗？请加以证明．
  【拓展提高】（3）如图3，若等腰直角△ABC绕点B逆时针旋转，当EC恰好与BD平行时，（1）中得到的结论还成立吗？请加以证明．
  组卷：296引用：6难度：0.1

  解析