综合与实践：
已知△ABC与△BDE均为等腰直角三角形，其中∠BAC=∠BDE=90°，连接CE，P是EC的中点，连接PA，PD．
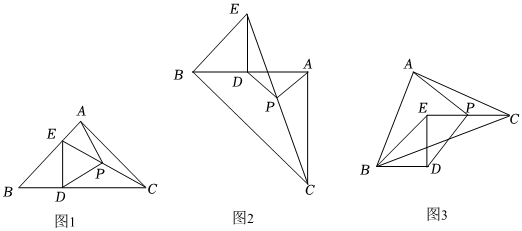
【初步感知】（1）如图1，当B，D，C三点在同一直线上时，PA和PD的数量关系为 PA=PDPA=PD，位置关系为 PA⊥PDPA⊥PD．
【深入探究】（2）如图2，当B，D，A三点在同一直线上时，（1）中得到的结论成立吗？请加以证明．
【拓展提高】（3）如图3，若等腰直角△ABC绕点B逆时针旋转，当EC恰好与BD平行时，（1）中得到的结论还成立吗？请加以证明．
【考点】几何变换综合题．
【答案】PA=PD；PA⊥PD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 20:0:1组卷：296引用：6难度：0.1
相似题
-
1．如图，在矩形ABCD中，AD=26，AB=48，点E是边AB上的一个动点，将△CBE沿CE折叠，得到△CB'E连接AB'，DB'，若△ADB'为等腰三角形，则BE的长为 ．发布：2025/5/23 11:0:1组卷：366引用：2难度：0.3 -
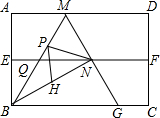2．如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：
①∠ABN=60°；②AM=1；③QN=；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是33．3
其中正确结论的序号是．发布：2025/5/23 1:30:2组卷：3126引用：15难度：0.5 -
3．在△ABC中，AB=AC，∠BAC=α，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，连接DB，DC．
（1）如图1，当α=60°时，
①求证：PA=DC；
②求∠DCP的度数；
（2）如图2，当α=120°时，请直接写出PA和DC的数量关系．
（3）当α=120°时，若AB=6，BP=，请直接写出点D到CP的距离为．31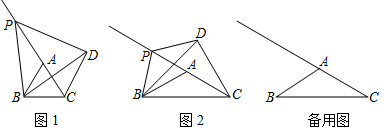
发布：2025/5/23 4:0:1组卷：4734引用：13难度：0.1
