2022-2023学年四川省成都三十八中高一(下)期中数学试卷
发布:2024/7/9 8:0:8
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符题目要求的.
-
1.计算sin48°cos18°-cos48°cos72°的结果等于( )
组卷:211引用:2难度:0.8 -
2.已知
,则tan2α=( )tanα=12组卷:120引用:3难度:0.8 -
3.已知向量
,且a=(2,3),b=(1,x),则向量a⊥b=( )2a+3b组卷:215引用:3难度:0.9 -
4.在平行四边形ABCD中,
,CF=12CD,设CE=2EB,则x+y=( )EF=xAB+yAD组卷:74引用:3难度:0.7 -
5.下列直线中,可以作为曲线
的对称轴的是( )y=cos(2x-π2)组卷:249引用:4难度:0.6 -
6.在△ABC中,已知sinA:sinB:sinC=5:7:8,则△ABC中最大角的余弦值为( )
组卷:96引用:2难度:0.7 -
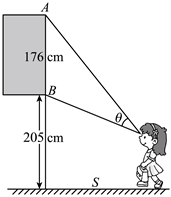 7.2023年是农历癸卯兔年,在中国传统文化中,兔被视为一种祥瑞之物,寓意福寿安康.故宫博物院就收藏着这样一副蕴含“吉祥团圆”美好愿景的名画——《梧桐双兔图》,该绢本设色画纵约176cm,横约95cm,其挂在墙壁上的最低点B离地面205cm.小南眼睛距地面的距离为150cm,为使观赏视角θ最大,小南离墙距离S应为( )组卷:62引用:4难度:0.5
7.2023年是农历癸卯兔年,在中国传统文化中,兔被视为一种祥瑞之物,寓意福寿安康.故宫博物院就收藏着这样一副蕴含“吉祥团圆”美好愿景的名画——《梧桐双兔图》,该绢本设色画纵约176cm,横约95cm,其挂在墙壁上的最低点B离地面205cm.小南眼睛距地面的距离为150cm,为使观赏视角θ最大,小南离墙距离S应为( )组卷:62引用:4难度:0.5
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.
-
21.已知△ABC的内角A,B,C的对边分别为a,b,c,若(sinB-sinC)2=sin2A-sinBsinC,
.a=3
(1)求A;
(2)若△ABC为锐角三角形,求b-c的取值范围.组卷:112引用:2难度:0.5 -
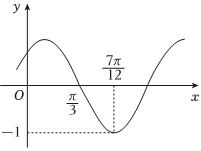 22.已知函数的部分图像如图所示.f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)
22.已知函数的部分图像如图所示.f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)
(1)求函数y=f(x)的解析式;
(2)将y=f(x)的图像上所有点的横坐标缩短到原来的,纵坐标不变,再向右平移12个单位长度得到y=g(x)的图像,求函数g(x)的单调递增区间;π6
(3)在第(2)问的前提下,对于任意,是否总存在实数x1∈[-π3,π3],使得f(x1)+g(x2)=m成立?若存在,求出实数m的值或取值范围;若不存在,说明理由.x2∈[-π6,π6]组卷:335引用:8难度:0.5


