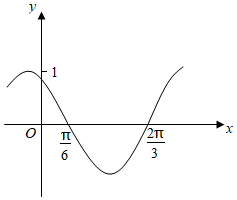
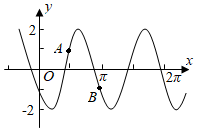
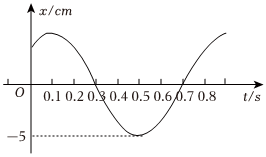
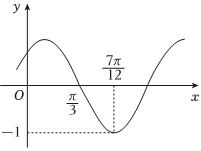
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图像如图所示．
（1）求函数y=f（x）的解析式；
（2）将y=f（x）的图像上所有点的横坐标缩短到原来的12，纵坐标不变，再向右平移π6个单位长度得到y=g（x）的图像，求函数g（x）的单调递增区间；
（3）在第（2）问的前提下，对于任意x1∈[-π3，π3]，是否总存在实数x2∈[-π6，π6]，使得f（x1）+g（x2）=m成立？若存在，求出实数m的值或取值范围；若不存在，说明理由．
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
1
2
π
6
x
1
∈
[
-
π
3
，
π
3
]
x
2
∈
[
-
π
6
，
π
6
]
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/9 8:0:8组卷：330引用：8难度：0.5
